Introduction
The effective use of vortex energy in the production of strong velocity fields by the different devices is one of the modern areas of applications, developed during the last years, an example is the RKA (ReaktionsKraftAnlage) used on the cars’ roofs for substations reducing the air's drag [1,2] (Figure 1), in the area for obtaining large velocity fields [3,4].
Figure 1: The cars' roofs.
In 2004 A.Bertasius, A.Buikis, and P.Verzbovicius formulated a patent [5] of apparatus and methods for heat generation. Later A.Buikis and H.Kalis have constructed a mathematical model of this heat generator [6-8].
In this model, the viscous electrically conducting incompressible liquid is located between two infinite coaxial cylinders (rings). The electromagnetic force drives magneto-hydrodynamic flow between the cylinders.
In 2009 designed a similar generator to [9] and created a mathematical model for the generator [10,11]. In the internal cylinder parallel to the axis are placed metal conductors-electrodes of the forms of bars. For those conductors, the alternating current is connected. The water is a weakly electrically conducting liquid (electrolyte). This is the mathematical model of one device for electrical energy produced by alternating current in the production of heat energy.
The distribution of electromagnetic fields, forces, 2D magnetohydrodynamic flow, and temperature induced by the system of the alternating electric current or external magnetic field in a conducting cylinder has been calculated using finite difference methods. An original method was used to calculate the mean values of electromagnetic forces.
The second interesting way in the vortexes exploitation in devices was collaboration with inventor J. Schatz in Germany [12,13]. In new technological applications, it is important to use vortex distributions for obtaining large values of velocity. The effective use of vortex energy in the production of strong velocity fields by different devices is one of the modern areas of applications, developed during the last decade. Such processes are ecologically clean; there is no environmental pollution. Although, on the other hand, the aspect of energy is very important: the transformation process should be organized in such a way that vortex energy is effectively transformed into heat or mechanical energy. In our previous papers [6,7,14,15] we have mathematically modeled the process how transforming the alternating electrical current into heat energy.
The practical aim of this investigation is to try to understand the process in the element of Hurricane Energy Transformer. This element is a central figure in the so-called RKA (German: ReaktionsKraft Anlage, English: Reaction Force Device) used on the cars’ roof for substation reducing the airs’ drag. This is all that's done at the practical level in mathematical modeling.
However, several practical and theoretical questions are left unanswered. Devices sometimes have worked with effectiveness higher than 100 Important is that in such a system there are strong vortices and electromagnetic fields or high velocities. For example, in [5,9] the alternating electro currency with voltage 380 V is about 1 ampere on 1 cm. Theoretically, the answer may be that we have a contradiction in the macro and micro processes in such devices [16].
Following Kim [17], we require a new paradigm beyond materialism including the information field on the theory of Physical vacuum. It is easy to call such science pseudoscience, but within its framework, it is possible to portray scalar waves [18,19]. In recent years, there have been several other new approaches: space-time as energy [19]. We should discuss these approaches with an open mind, without a simple rejection.
The goal of this paper is to develop mathematical models for new types of ecologically clean and energetically effective devices [12,20-23].
Such a type of device firstly was developed by I. Rechenberg [1]. Now the continuator of the work is one of the authors J. Schatz. The devices of such type can be considered as the energy source of the new generation. The practical aim of this investigation is to try to understand the process in the element of Hurricane Energy Transformer [12]. This element is the central figure in so so-called RKA (ReaktionsKraftAnlage) used on the cars’ roof for substation reducing the air’s drag.
This work presents three mathematical models of such devices. It is
- a finite cylinder with a finite number of circular vortex lines positioned on its inner surface with a fixed distance between each other,
- a finite cylinder or cone with a finite number of spiral vortex threads positioned on its inner surface,
- a plane channel with a finite number of linear vortex lines positioned on its boundary.
It is well known that the vortex theory began from the Decart papers. First of all, it investigated the behavior of the discrete N linear vortex lines with an equal intensity Γ, which are in the vertices of the regular rectangle (authors are Helmholc, Kelvin, Kirhof, see [24-26]). The investigation of contemporary is written in the books [27,28]:
Completely are investigated linear vortex lines, vortex sheets, vortex wakes, vortexes of Karman, but difficulties cause the curves of vortex lines. In new technological applications, it is important to use vortex distributions for obtaining large values of velocity.
The mathematical model
Let the cylindrical domain (conus)
contain ideal incompressible fluid,
where a, Z the maximal radius and length of the cylinder, M is the number of circulation periods.
If ∈ = 0; then we have the circular cylinder with the radius a.
Consider the situation when the N discrete circular vortex lines
with intensity
and radii ai(m) are placed in the cylinder.
The vortex creates in the ideal compressible liquid the radial vr and axial vz components of the velocity field, which rises to the liquid motion.
Similar can be considered N discrete spiral vortex threads
with parameters
Here τ is the rise of the vortex threads, the spiral vortex with Z=2π, a=1, N=6, M=1, τ=1, ∈=0;1.
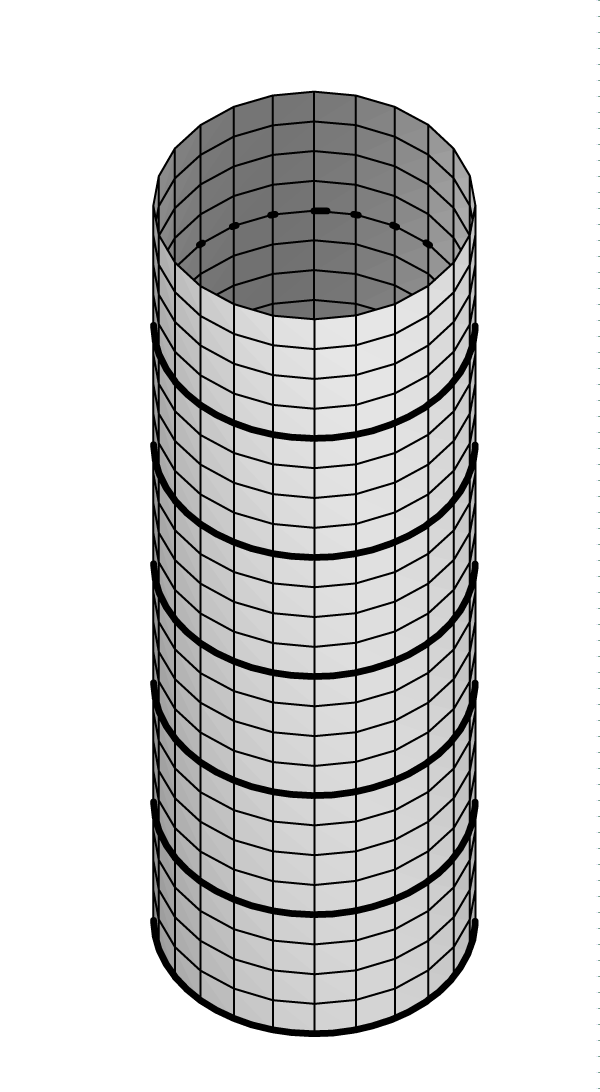
In the Figure 2, we can see the circular vortex lines.
Figure 2: The surface of the cylinder with circular vortex lines.
The spiral vortexes create in the ideal compressible liquid the radial vr, axial vz, and azimuthal vϕ components of the velocity field.
The linear vortex lines create in the plane domain-channel
the vx,vy components of the velocity field.
The main aim of this work is to analyze the diversity of connection schemes of vortex curves that influence the maximal value of velocity.
Calculation of the velocity field for the spiral vortexes
The vector potential A is determined from the equations of vortex motion of ideal incompressible fluid [12,20,22,25,26]
in the following form:
where v = rotA and v,Ω the vectors of velocity and vortex fields are, ∆ is the Laplace operator.
Applying the Biot-Savar law [25,26] we receive the following form of the vector potential created by the vortex thread Wi (Wi= Si or Wi= Li):
where dl is an element of the curves, P=P(x,y,z) is the fixed point in the liquid, Q=Q(ξ,η,ζ) is the changeable point in the integral
From cylindrical coordinates x=rcosϕ, y=rsinϕ,
for the spiral vortexes Si:
and we have the following components of the vector potential:
where
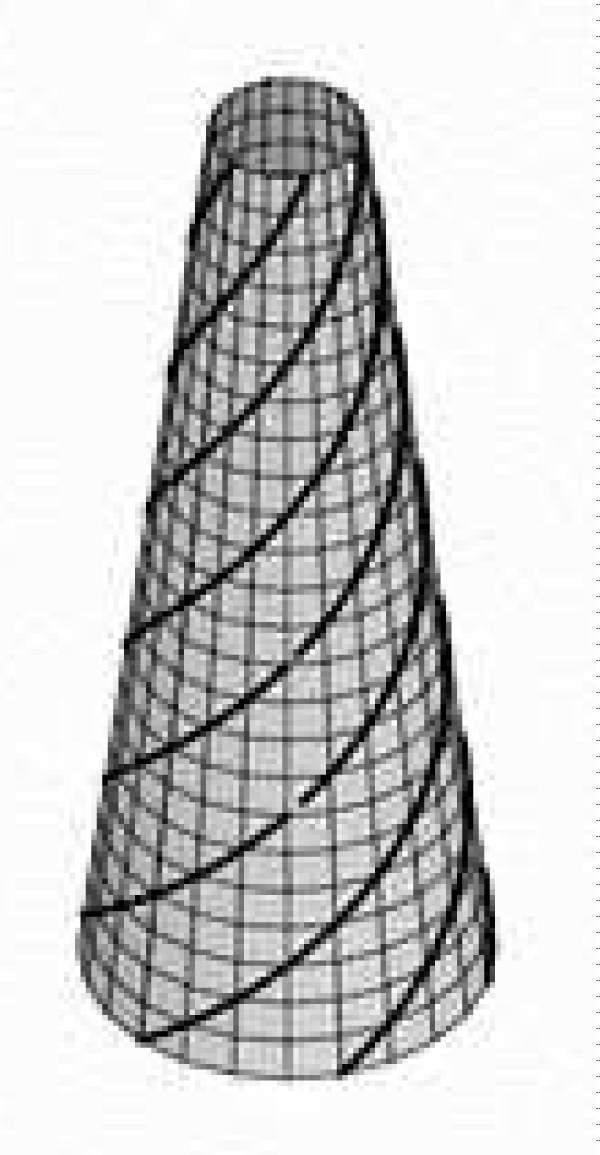
(Figure 3).
Figure 3: Spiral vortices on the cone with ∈ − 0.1,
Z = 2π .
Therefore
and
The vector components of the velocity field (radial, axial, azimuthal) induced by the spiral vortex curves are in the form
where
are the radial and azimuthal components of vector potentials.
Then from the partial derivatives
follows
For ∈ = 0 and for the symmetrical properties respect to z=z/2 follows that for the all components of velocity
If r=0, then
or
Therefore, from [24]:
Where
If ∈=0, then
and the maximal value of velocity is
by z=Z/2.
The minimal value we have in the form
By z=0 and z=Z
The averaged value of the axial component of the velocity field in the axes of the cylinder (r=0) is
The average value ∈=0, r=0 is
From I. Rechenberg [1] (∈=0) in the middle point of finite vortex spool (z=Z/2) with the length Z the axial component of one vortex thread is
where
β is the rise of vortex thread angles (β=arctan(τ)) and D = 2a is the diameter of the vortex spool.
For the minimal value of velocity ( in the points z=0 und z=Z) [1]:
We have equal values of vmax from (11) and from (7) using
The average value (10) for ∈=0 is in the following form
where
.
In the formulas parameters M and Z are depending:
Therefore from (4) (13) for the velocity components (vτ,vz,vϕ) and the azimuthal component of the vector potential Aϕ
induced by N discrete vortex are
Integrals are with the trapezoid formulas calculated.
If the intensity Γi of N - the spiral vortex Si is equal Γ, then from (6) - (12) follows:
where N - the number of vortex threads, H=Z- and the height of the vortex spool (in building synonym of the length) are.
For the averaged value of velocity, (∈=0) we have the formula
or
where
If the averaged value vav is known, then it can be calculated from (19) also the dimensionless length
in the following form
where
An example, if
then δ = 1.452 and y = 2.62, z=0.3275(m).
The corresponding formulas (15, 17); (16,18), and (19, 20) are identical, but from (15),(16), and (19) follows, that the velocity depending on the parameter M*N is, where
From (15, 16) and (19) we can find the corresponding multiplicators by
calculating (Table 1):
and
Calculation of the velocity field for the circular vortex lines
For the circular vortex lines:
and from axially-symmetric condition follows that by ϕ = 0 is Ax, i = Az,i = 0 and
where
The integral ιi is equal [25]
where
is the total elliptical integral of the first kind,
is the total elliptical integral of the second kind.
Therefore the azimuthal component of vector potential Ai induced by a circular vortex line Li with intensity Γ, and radius ai is
The vectorial components of the velocity field (the radial and axial components) induced by the vortex line Li are
or
If r = 0 then
This component of vectors has the maximal value
by z=zi, ai=a.
By z=zi+Z/2 we have
this is the value of the component of velocity induced by a spiral vortex (∈=0).
If z=Z/2, ai=a then from (24) follows
For the averaged value of the velocity we have
If zi = Z/2, then
The summary velocity field (vr,vz) and the vector potential Aϕ induced by N discrete vortex lines we obtained in the form (14). The hydrodynamic stream function ψ = ψ(r,z) for velocity components
from (21) is
The amount of flow through the cross-section [z=z0,0
The total amount of flow through cross cylindrical domain
[0
For the circular vortex line, if
we can calculate the following multiplicators by the factor
for (25),
for (26).
An example, if Z/a = 1.4 then we can the multiplicators
R4((0), R4(Z/2),R4(Z),R5 for the circular vortex lines and R1,R2,R3 for the spiral vortexes, by the factor in the form R1*N R2*N R3*N calculated (Table 1).
| Table 1: Multiplicators of the velocity for vortexes by
. |
| N |
R4 (0) |
R4 (Z / 2) |
R4 (Z) |
R5 |
R1 |
R2 |
R3 |
| 1 |
0.94 |
0.71 |
0.26 |
0.69 |
0.82 |
0.58 |
0.74 |
| 2 |
1.74 |
1.59 |
0.62 |
1.46 |
1.64 |
1.16 |
1.47 |
| 3 |
2.37 |
2.58 |
1.09 |
2.27 |
2.46 |
1.74 |
2.21 |
| 4 |
2.85 |
3.56 |
1.72 |
3.09 |
3.28 |
2.32 |
2.94 |
| 5 |
3.20 |
4.44 |
2.52 |
3.85 |
4.10 |
2.91 |
3.68 |
| 6 |
3.47 |
5.16 |
3.47 |
4.55 |
4.92 |
3.48 |
4.41 |
In the following calculations we use the dimensionless form scaling all the lengths to r0 = a (the inlet radius of the tube), the axial vz and radial vr velocity to
the azimuthal components of vector potential Aϕ to
, the stream function ψ to ψ0 =A0r0 and the total amount of flow Q to Q0=ψ0r0. Here Γ0 is dimensional scaling of vortex intensity
The flow field induced by linear vortex lines in a channel
Unlike our previous papers [20,21] here we additionally consider the chain of linear vortex lines in the plane channel. For symmetry-conditions,
we consider half the plane channel y ∈ [0,1].
In the plane, y=0 we have the slip conditions vx=vy=0 for the velocity vectors of viscous incompressible liquid.
The flow in the channel is given by a fixed amount of flow through a cross-section of the half-channel
If L=∞, then vx =u(y),vy = 0 we have the Puaseil flow u = Q(3y-1.5y2) - the solution of Navier-Stokes equation in the channel Ωx,y.
The wall y=0 of the channel is placed in a linear chain of vortexes with the axis transfer of the (x,y) plane. The one linear vortex line in the point (xk,yk)) creates the following components of velocity:
where
In the center of this point-wise vortex, the velocity field is infinite therefore we consider the vortex line with the finite cross-section
the circle with radius a. In this case the expressions (27) are valid when R≥a. but for R< a we have
Some numerical results and discussion
The flow in the channel
We consider the channel with finite length L = 2.5, Puaseil flow with Q=3 and three wise of the chain of vortexes:
1) the main chain with coordinates and radius of the linear vortex
rotate clockwise with the intensity Γ1,
2) the second chain with coordinates and radius of the linear vortex
rotate opposite clockwise with the intensity Γ2,
3) the thread chain with coordinates and radius of the linear vortex
rotate opposite clockwise with the intensity Γ3.
For the pointwise vortexes line (29) outside the channel (yk = -0.025) Γ1 = -6 we have the following results: mV = 5.9895, mX = 1.00, mY = 0.
For the Karman chain [25] of vortexes (preliminary vortexes line and (30) we have mV = 3.9790, mX = 0.20, mY = 0.
In the following Table 2 can see the amount maximal value of velocity u,(mv) with the coordinates (mX,mY) depending on the vortex intensity Γ1, Γ2, Γ3
| Table 2: The dependence of flow velocity on the intensity of the vortexes. |
| Γ1 |
Γ2 |
Γ3 |
Q |
mV |
mX |
mY |
| 0 |
0 |
0 |
3.00 |
4.500 |
0.00 |
1.00 |
| -6 |
3 |
3 |
3.97 |
18.19 |
2.20 |
0.15 |
| -6 |
4 |
4 |
3.46 |
22.90 |
0.30 |
0.10 |
| -6 |
3 |
0 |
4.62 |
18.36 |
0.20 |
0.15 |
| -6 |
2 |
2 |
4.49 |
18.63 |
2.20 |
0.15 |
| -6 |
1 |
1 |
5.00 |
19.08 |
2.20 |
o.15 |
| -6 |
1 |
0 |
5.22 |
19.14 |
0.20 |
0.15 |
| -6 |
0 |
1 |
5.30 |
19.47 |
2.20 |
0.15 |
| -6 |
0 |
0 |
5.52 |
19.86 |
1.00 |
0.15 |
The circular vortexes lines
The basis for the calculations of N circular vortex lines
are N≤ 6 chosen, which are arranged in the axial direction at the points with the following dimensionless coordinates
The dimensionless radius of the circular vortex lines ai is considered in three forms (the sequence a = [a1, a2, a3, a4, a5, a6,]):
- the constant sequence( radius of the cylinder) ac = [1,1,1,1,1,1],
- the monotonous increasing sequence ain = [.75,.80,.85,.90,.95,1.0],
- the monotonous decreasing sequence ad = [1.0,.95,.90,.85,.75],
The results of numerical experiments for dimensionless values vr,vz,ψ,Qt was obtained of different dimensionless intensity of vortex lines
The summary intensity of absolute values is equal to 6.
The velocity field is calculated on the uniform grid (nr×nz) by the steps h1=h2=0.1 in the r,z directions.
The numerical results show that the velocity field induced by circular vortex lines is concentrated inside the cylinder. The results depend on the arrangement and the radius of vortex lines ai.
Typical results of calculations are the dimensionless velocity field and the distribution of stream function in the cylinder. We can see the velocity formation depends on the arrangement of vortice lines with coordinates zj=[z1,z2,z3,z4,z5,z6], and of the radii ai.
If
then all vortices move in the positive direction of Oz axis (vz >0), but the radii of vortex lines to stay a different way (for vr<0 the radius is decreasing and for vr>0 the radius is increasing).
We obtain the dimensionless values of
for zj = [0.2,0.4,0.6,0.8,1.0,1.2] and for different radius of vortex lines ai and sequence of intensity gj=[g1,g2,g3,g4,g5,g6] the following results:
1. The radii are constant ac = [1,1,1,1,1,1]
1.1 The intensity of the one vortex line L3 is
vr∈(-5.9,5.9), vzmax = 18.85, ψmax = 3.25,
vr = 0 if z=z3 = 0.6 and vr>0 if z>z3, therefore the radius of the vortex increased [26];
1.2 The intensity of the one vortex line L3 is
(in the opposite direction):
vr∈(-5.9,5.9), vzmax = -18.85, ψmax = - 3.25,
the vortex moves in the negative direction of the Oz axes (vz0), vr = 0 if z=z3 = 0.6 and vr > 0 if z z3, therefore the radius of the vortex also increases [26];
1.3 The intensity of the two vortex lines L3,L4 are
vr∈(-5.7,5.7), vzmax = 18.57, ψmax = 3.17,
the vortexes move in the positive direction of Oz axes (vz > 0), vr = 0 if z=(z3+z4)/2=0.7 and vr(a0,z3) = -2.46, vr(a0,z4) = 4.37, therefore the radius of the first vortex lines L3 decreased, but for the second vortex lines L4 increased and the first vortex can be move through the second vortex [26];
1.4 The intensity of the two vortex lines L3,L4 are
vr∈(-2.9,0.64), vz∈(-3.0,3.0), ψ∈(-0.32,0.32),
vz = 0 if z = 0.7 and vz(a0,z3)=-1.72, vz(a0,z4) = 2.76, therefore the first vortex moves to the negative direction, but the second to the positive direction of Oz axes and the radii of the vortexes decreased (this case is in [26] considered);
1.5 The intensity of the two vortex lines L3,L4 are
vr∈(-0.64,2.9), vz∈(-3.0,3.0), ψ∈ (-0.32,0.32),
vz = 0 if z = 0.7 and vz(a0,z3)=1.72, vz(a0,z4) = -2.76, the first vortex moves to the positive direction, but the second to the negative direction of Oz axes and the radius of the vortexes increases [26];
1.6 The intensity of the three vortex lines L1,L3,L5 are
vr∈(-4.1,4.1), vzmax = 16.34, ψmax = 2.63,
vr = 0 if z=z3 = 0.6 and vz(a0,z1)=15.92, vz(a0,z3)=16.16, vz(a0,z5)=15.92, vr(a0,z1)=-3.8, vr(a0,z5)= 1.6, the vortexes move in the positive direction of Oz axis and the radius of the first vortex decreased, but of the third vortex increased;
1.7 The intensity of the three vortex lines
are
vr∈(-1.6,1.6), vzmin = -5.83, ψmin = -0.74,
vr = 0 if z=z3=0.6, z=0.1, z=1.1 and vz(a0,z1)=-5.67, vz(a0,z3)=-2.42, vz(a0,z5)=-3.56, vr(a0,z1)=-0.77, vr(a0,z5)=0.77, the vortexes move in the negative direction of Oz axis and the radius of the first vortex decreased, but of the third vortex increased;
1.8 The intensity of the three vortex lines L1,L3,L5 are
vr∈(-1.6,1.6), vz.max = -5.83, ψmax = 0.74,
vr = 0 if z=z3=0.6, and vz(a0,z1)=5.67, vz(a0,z3)=1.97, vz(a0,z5)=5.67, vr(a0,z1)=0.77, vr(a0,z5)=-0.77, the vortexes move in the positive direction of Oz axis and the radius of the first vortex increased, but of the third vortex decreased;
1.9 The intensity of the three vortex lines L1,L3,L5 are
vr∈(-4.9,2.6), vz∈(-1.75,11.1), ψ∈(-0.10,1.45),
vr = 0 if z= 0.9 and vz(a0,z1)=-0.64, vz(a0,z3)=8.28, vz(a0,z5)=10.89, vr(a0,z1)=-3.17, vr(a0,z3)=-3.95, vr(a0,z5)= 0.77, the two vortexes L3,L5 move in the positive direction, but the first in the negative direction of Oz axis and the radii of the two vortexes L1,L3 are decreased, but of the third vortex increased;
1.10 The intensity of the three vortex lines L1,L3,L5 are
vr∈(-2.6,4.9), vz∈(-1.75,11.1), ψ∈(-0.10,1.45),
vr = 0 if z = 0.3 and vz(a0,z1)= 10.89, vz(a0,z3)=8.28, vz(a0,z5)=-0.64, vr(a0,z1)=-0.77, vr(a0,z3)= 3.95, vr(a0,z5)= 3.17, the two vortexes L1,L3 move in the positive direction, but the vortex L5 in the negative direction of Oz axis and the radii of the two vortexes L3,L5 are increased, but of the third vortex L1 decreased;
1.11 The intensity of the three vortex lines L1,L3,L5 are
vr∈(-4.9,2.6), vz∈(-11.1,1.75), ψ∈(-1.45,0.10),
vr = 0 if z = 0.3 and vz(a0,z1)= -10.89, vz(a0,z3)=-8.28, vz(a0,z5)=0.64, vr(a0,z1)=0.77, vr(a0,z3)=-3.95, vr(a0,z5)= -3.17, the two vortexes L1,L3, move in the negative direction, but the third in the positive direction of Oz axis and the radii of the two vortexes L3,L5 are decreased, but of the first vortex increased.
2. The radii are increasing ain,
2.1 The non-uniform distribution of intensity gj = [2,2,1,.5,.5,0], N=5:
vr∈(-12.7,7.4), vz.max = 21.15, ψmax = 4.6, Qt = 28.34,
vr = 0 if z = 0.3, the radius of the first vortex decreased, but increased the radii of the last four vortexes ;
2.2 The distribution of intensity gj = [2,2,2,0,0,0], N=3:
vr∈(-13.3,10.02), vz.max = 22.23, ψmax = 4.8, Qt = 28.69,
vr = 0 if z = 0.3, the radius of the first vortex decreased, but increased the radii of the last vortex ;
2.3 The distribution of intensity gj = [0,0,3,3,0,0], N=2:
vr∈(-10.2,9.4), vz.max = 21.14, ψmax = 4.64, Qt = 29.20,
vr = 0 if z = 0.7, the radius of the first vortex decreased, but increased the radii of the last vortex ;
2.4 The intensity of the first vortex lines gj = [6,0,0,0,0,0], N=1:
vr∈(-19.2,19.2), = 25.13, ψmax = 6.47, Qt = 27.10,
vr = 0 if z = 0.2, the radius of the vortex increased;
2.5 The intensity of second vortex lines gj = [0,6,0,0,0,0], N=1:
vr∈(-15.0,15.0), vz.max = 23.56, ψmax = 5.69, Qt = 29.28,
vr = 0 if z = 0.4, the radius of the vortex increased;
2.6 The intensity of third vortex lines gj = [0,0,6,0,0,0], N=1:
vr∈(-11.8,11.8), vz.max = 22.18, ψmax = 5.11, Qt = 29.69,
vr = 0 if z = 0.3, the radius of the vortex increased;
2.7 The intensity of fourth vortex lines gj = [0,0,0,6,0,0], N=1:
vr∈(-9.6,9.6), vz.max = 20.94, ψmax = 4.66, Qt = 28.72,
vr = 0 if z = 0.3, Hence, the radius of the vortex increased.
3. The uniform distribution of intensity gj = [1,1,1,1,1,1]
3.1 Radii of vortex lines are constant (the sequence ac:
vr∈(-4.5,4.5), vz.max = 16.21, ψmax = 3.14, Qt = 25.12,
vr = 0 if z = 0.7, the radii of the first three vortexes decreased, but of the last three vortexes increased ;
3.2 Radii of vortex lines are ain:
vr∈(-8.4,4.9), vz.max = 17.98, ψmax = 3.52, Qt = 27.36,
vr = 0 if z = 0.8 the radii of the first three vortexes decreased but of the last two vortexes increased;
3.3 Radii of vortex lines are ad:
vr∈(-4.9,8.4), vz.max = 17.98, ψmax = 3.52, Qt = 27.36,
vr = 0 if z = 0.5 the radii of the first two vortexes decreased but increased the radii of the last four vortexes.
4. The distribution of intensity gj = [2,2,.5,.5,.5,.5]
4.1 Radii of vortex lines are ain:
vr∈(-12.3,6.9), vz.max = 20.19, ψmax = 4.4, Qt = 27.77,
vr = 0 if z = 0.3, the radius of the first vortex decreased but increased the radii of the last five vortexes;
4.2 Radii of vortex lines are ad:
vr∈(-5.7,5.6), vz.max = 17.30, ψmax = 3.4, Qt = 26.0.1,
vr = 0 if z = 0.4, the radius of the first vortex decreased but increased the radii of the last four vortexes.
5. The distribution of intensity gj = [.5,.5,.5,.5,.5,2,2]
5.1 Radii of vortex lines are ain:
vr∈(-5.6,5.8), vz.max = 17.30, ψmax = 3.4, Qt = 26.0.1,
vr = 0 if z = 1.0, the radii of the first four vortexes decreased but increased the radius of the last vortex;
5.2 Radii of vortex lines are ad:
vr∈(-6.8,12.3), vz.max = 20.19, ψmax = 4.4, Qt = 27.7.7,
vr = 0 if z = 1.1, the radii of the first five vortexes decreased, but those of the last vortex increased.
6. The distribution of intensity gj = [.5,.5,2,2,.5,.5]
6.1 Radii vortex lines are ain:
vr∈(-7.4,6.6), vz.max = 19.47, ψmax = 4.0, Qt = 28.28,
vr = 0 if z = 0.7 the radii of the first two vortexes decreased but increased the radii of the last four vortexes;
6.2 Radii of vortex lines are ad:
vr∈(-6.6,7.4), vz.max = 19.47, ψmax = 4.0, Qt = 28.28,
vr = 0 if z = 0.7 the radii of the first two vortexes decreased but increased the radii of the last four vortexes.
6.3 The spiral vortexes in the cylinder (∈=0)
We consider N≤6 spiral vortexes
, which started from the points (a,0,i2π/N) at the cylinder.
The dimensionless radius of the cylinder a is equal to 1.
All results of the numerical experiments are for the dimensionless values Aϕ(a0,z,ϕ),vz(0,z),Q(z),Qt and parametern l=Z/a =0.5;1;1.5;2;3, a0 = 0.7 obtained.
The summary intensity of absolute values is equal to 6.
The azimuthal components of the vector potential are in the uniform grid (Nz×Nϕ) by the steps hz = l/ Nz, hϕ = 2π/Nϕ,(Nz= Nϕ = 30) in the r,ϕ direction calculed.
The component Aϕ(z,ϕ)=(r=a0) using the trapezoid formula is calculated. Figures show typical results of calculations: the dimensionless velocity field and the distribution of the azimuthal component of the velocity (r=a0) in the cylinder.
The velocity formation depends on the length / of the cylinder.
The maximum of the azimuthal components of vector potentials Amax is depending of the intensity parameter
We obtain the dimensionless values of vz.max,Qmax,Amax,Qt, and for different sequence of intensity gj=[g1,g2,g3,g4,g5,g6] the following results:
1. The length is ι =1.5,
(vz.max = 15.08, Qmax = 24.98, Qt = 33.20)
1. The uniform distribution of the intensity
gj = [1,1,1,1,1,1], N=6: Amax = 5.68,
the distribution Aϕ is uniform in the ϕ direction;
2. The distribution of the intensity is gj = [2,2,1,.5,.5,0], N = 5:
Amax = 5.68, the distribution of Aϕ is nonuniform in the ϕ direction;
3. The distribution of the intensity is gj = [2,2,2,.0,0,0], N = 3:
Amax = 5.75, the values of Aϕ oscillate in the ϕ direction;
4. The distribution of the intensity is gj = [2,1,1,1,1,0], N = 5:
Amax = 6.14, the distribution of Aϕ is nonuniform in the ϕ direction; (the maximal value 6.14 is in the point (0.75,4.2);
5. The distribution of the intensity is gj = [1.5,1.5,1.5,1.5,0,0], N = 4:
Amax = 5.68, the values of Aϕ weakly oscillate in the ϕ direction;
6. The distribution of the intensity is gj = [3,3,0,0,0,0], N = 2:
Amax = 5.83, the distribution of Aϕ is nonuniform in the ϕ direction with 3 maximums;
7. The distribution of the intensity is gj = [6,0,0,0,0,0], N = 1:
Amax = 8.54, the distribution of Aϕ is nonuniform in the ϕ direction with one maximum;
8. The distribution of the intensity is gj = [6,0,0,0,0,0], N = 1, b=0;
Amax = 8.40, vz.max = 18.85, Qmax = 36.95, Qt = 24.54 the distribution Aϕ is uniform in the ϕ direction (this is the velocity field induced by the circular vortex line (zi = 0)).
2. Different lengths ι
1. The distribution of the intensity is gj = [6,0,0,0,0,0], N = 1:, l=1.
Amax = 8.42, vz.max = 18.29, Qmax = 36.25, Qt = 16.28;
2. The distribution of the intensity is gj = [2,2,1,.5,.5,0], N = 5, ι =3:
Amax = 5.11, vz.max = 10.46, Qmax = 16.36, Qt = 43.03;
3. The distribution of the intensity is gj = [2,2,1,.5,.5,0], N = 5, ι =2:
Amax = 6.0386, vz.max = 13.3285, Qmax = 21.4252, Qt = 37.6009,
If Nϕ = Nz = M = 50, then Amax = 6.0386, vz.max = 13.3286, Qmax = 21.4252, Qt = 37.6017;
The distribution of the intensity is gj = [2,2,1,.5,.5,0], N = 5, ι =1:
Amax = 7.35, vz.max = 16.86, Qmax = 29.39, Qt = 26.65,
5. The distribution of the intensity is gj = [2,2,1,.5,.5,0], N = 5, ι = 5:
Amax = 8.11, vz.max = 18.29, Qmax = 34.25, Qt = 16.28,
6.4 The spiral vortexes in the cones (∈≠0)
In this case, we have some results for the behavior of spiral vortexes.
1. If
then from the formulas (14, 18) can be the values
calculated (Table 3).
| Table 3: The velocity Vav by a = 0.125. |
| Z |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
| M |
0.72 |
1.44 |
2.17 |
2.89 |
3.61 |
4.33 |
5.06 |
5.78 |
6.50 |
7.22 |
| V1 |
15.3 |
24.1 |
29.0 |
32.0 |
34.0 |
35.4 |
36.5 |
37.3 |
37.9 |
38.5 |
| V2 |
15.5 |
24.6 |
29.7 |
32.7 |
34.8 |
36.2 |
37.3 |
38.2 |
38.8 |
39.4 |
| V3 |
15.7 |
25.1 |
30.3 |
33.5 |
35.6 |
37.1 |
38.2 |
39.1 |
39.8 |
40.4 |
| V4 |
14.9 |
23.3 |
27.9 |
30.7 |
32.6 |
33.9 |
34.9 |
35.7 |
36.3 |
36.8 |
For
and
the radii by
decreased from
with
and
, but for
the radius increased with
.
2. If
, then similar to the formulas (9, 20) can be the values
calculated (Table 4).
| Table 4: The velocity Vav by a = 0.25. |
| Z |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
| M |
0.36 |
0.72 |
1.08 |
1.44 |
1.80 |
2.17 |
2.53 |
2.89 |
3.25 |
3.61 |
| V1 |
4.19 |
7.64 |
10.2 |
12.1 |
13.5 |
14.5 |
15.4 |
16.0 |
16.6 |
17.0 |
| V2 |
4.27 |
7.86 |
10.6 |
12.6 |
14.0 |
15.2 |
16.0 |
16.7 |
17.3 |
17.8 |
| V3 |
4.34 |
8.10 |
11.0 |
13.1 |
14.6 |
15.9 |
16.8 |
17.6 |
18.2 |
18.7 |
| V4 |
4.06 |
7.23 |
9.54 |
11.2 |
12.4 |
13.4 |
14.1 |
14.7 |
15.2 |
15.6 |
For v2 and v3 the radii by z=1 decreased from a=0.25(m) with 0.16(m) and 0.07(m), but for v4 the radius increased with 0.43(m).
Conclusion
- Velocity fields of ideal compressible fluid influenced by a curved vortex field in a finite cylinder, finite cone, and channel are investigated.
- Numerical results show that the maximum axial velocity and the total amount of flow depend on the connection method of producers of vortex energy.
- The maximal velocity is developed in the case of non-uniform distribution of vortex intensity and smaller radius of vortex lines.
- The maximal value of the velocity induced by the spiral vortexes is in the middle of the cylinder.
- The behavior of vortex lines in the ideal incompressible flow depends on the number and the orientation of the vortex.
- The realization of circular vortices inside the pipe at the surface accelerates the flow speed inside the pipe if they rotate clockwise the flow depends on the values of parameters
and the inflow mode in the pipe.
- The calculations are related to specific applications of vortices in energy [21,23,26,25.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
 Help ?
Help ?




 Save to Mendeley
Save to Mendeley