Refinement of Jensen Mercer and Hermite–Hadamard-Mercer type inequalities for generalized convex functions on co-ordinates with their computational analysis

In the current study, the Jensen-Mercer inequality is extended to co-ordinated h-convex functions. Additionally, a novel inequality is employed to derive Hermite–Hadamard-Mercer type inequalities for h-convex functions defined on the co-ordinates of a rectangle in the plane. These developments not only reinforce the core tenets of convex analysis but also expand the applicability of Hermite-Hadamard-Mercer type inequalities to generalized convex functions on co-ordinates. This provides valuable tools for data analysis and optimization problem-solving. The practical utility and efficacy of this generalized inequality in real-world scenarios involving co-ordinates are demonstrated through a computational study.

Mathematics Subject Classification: 26D10, 26D15, 26A51, 34A08.

1. Introduction

Convexity is a fundamental concept in mathematics, particularly in the field of optimization and analysis. The history of convexity dates back to ancient times, with early mathematical investigations conducted by ancient Greek mathematicians such as Euclid and Archimedes. However, the formal development of convexity theory began to take shape in the 17th and 18th centuries with the works of mathematicians like Isaac Newton and Leonhard Euler.

In the 19th century, the concept of convexity saw significant advancements, particularly with the emergence of convex analysis. Augustin-Louis Cauchy, Jean-Victor Poncelet, and Joseph Fourier made notable contributions to the field during this period. The mid-20th century witnessed further progress in convex optimization and convex geometry, with mathematicians like Hermann Minkowski, George Dantzig, and John von Neumann playing pivotal roles in advancing the theory and applications of convexity.

Today, convexity theory is a cornerstone of mathematics, with widespread applications in various fields, including economics, engineering, computer science, and physics. Its importance stems from its elegance, versatility, and utility in modeling and solving a wide range of optimization problems.

The Hermite-Hadamard inequality, also known as the Hermite-Hadamard integral inequality, is a fundamental result in mathematical analysis that provides bounds on the value of certain types of integrals. It is named after French mathematician Charles Hermite and French mathematician Jules Henri Poincare (though it is often associated with the work of French mathematician Jacques Hadamard as well). Charles Hermite (1822-1901) was a prominent French mathematician known for his work in number theory, algebra, and mathematical analysis. He made significant contributions to the theory of elliptic functions, algebraic number theory, and mathematical physics. Jules Henri Poincare (1854-1912) was a leading mathematician and physicist who made substantial contributions to various fields of mathematics, including topology, celestial mechanics, and the theory of dynamical systems, to know more one can be seen [1,2]. Mathematically it is defined as:

If $Ϝ\mathrm{<mo>:</mo>}I\subset ℝ\to ℝ$ be a convex function on the interval I on the real numbers ${\sigma }_1\mathrm{,}{\varpi }_1\in I\mathrm{.}$ The inequality

$Ϝ\left(\frac{{\varpi }_1+{\sigma }_2}{2}\right)\le \frac{1}{{\varpi }_1-{\sigma }_1}{\displaystyle {\int }_{{\sigma }_1}^{{\varpi }_1}}Ϝ\left(\varkappa \right)d\varkappa \le \frac{Ϝ\left({\sigma }_1\right)+Ϝ\left({\varpi }_1\right)}{2}\mathrm{,}\text{ (1}\text{.1)}$

is known as Hermite-Hadamard inequality for convex function.

Breckner was the pioneer mathematician to introduce an s-convex function in 1979 [3], and the exploration of connections with s-convexity in its initial sense was extensively discussed in [4]. The direct proof of Breckner's seminal result was later acclaimed in 2001 by Pycia [5]. Given the pivotal role of convexity and s -convexity in unraveling optimality within mathematical programming, numerous researchers have dedicated substantial attention to s-convex functions. Notably, earlier works by H. Hudzik, et al. [4] elucidated two variants of s-convexity $s\in \mathrm{<mo\; stretchy="false">(</mo>0,1<mo\; stretchy="false">)</mo>}$ , demonstrating that the second sense inherently surpasses the s-convexity in the initial sense whenever $s\in \mathrm{<mo\; stretchy="false">(</mo>0,1<mo\; stretchy="false">)</mo>}$ . We broadly term the use of s-convexity in its second sense as an s-convex function. Given $s\in \mathrm{<mo\; stretchy="false">(</mo>0,1<mo\; stretchy="false">)</mo>}$ , this class of functions holds greater importance than convex functions. Moreover, our primary findings reveal that results obtained via s-convexity significantly outperform those derived from convexity. Additionally, s-convexity serves as a generalization of convex functions, allowing us to deduce results for convex functions by setting s=1 in the s-convex function outcomes. The Hadamard inequality for s-convex functions in its initial sense was introduced by S. S. Dragomir and Fitzpatrick [6]. Hadamard inequality for s-convex functions in the second sense was also introduced by S. S. Dragomir and Fitzpatrick in [6]. The class of h-convex functions was introduced by S. Varošanec in [7], which generalizes the concept of Convex Functions, s-Convex Functions, Godunova-Levin Functions, and p-Functions. Hadamard's type inequality for h-convex functions was introduced by Sarilaya, et al. in [8].

The primary objective and rationale behind coordinated convex functions lie in the fact that every convex mapping $Ϝ\mathrm{<mo>:</mo><mo\; stretchy="false">[</mo>}{\sigma }_1\mathrm{,}{\varpi }_1\mathrm{<mo\; stretchy="false">]</mo>}\to ℝ$ retains convexity when viewed along its coordinates. In other words, the function remains convex when examined individually along each coordinate axis. However, it's noteworthy that while coordinated convex functions exhibit this property, there also exist coordinated convex functions that are not globally convex. This highlights the nuanced relationship between coordinated convexity and global convexity, offering insights into the intricate nature of these mathematical structures (see for example [9,10]). For more results in the field of co-ordinated convex, we refer the interested readers to see [9-20].

S.S. Dragomir established the ensuing Hermite-Hadamard type inequalities for coordinated convex functions defined on the plane's rectangle  in [9].

Theorem 1

[9] Suppose that a function $Ϝ\mathrm{<mo>:</mo>}\Delta \mathrm{<mo>=</mo>}\left[{\sigma }_1\mathrm{,}{\varpi }_1\right]\times \left[{\sigma }_2\mathrm{,}{\varpi }_2\right]\subset {ℝ}^2\to ℝ$ is convex on co-ordinates. Then one has the inequalities:

$\frac{Ϝ\left({\sigma }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\sigma }_1\mathrm{,}{\varpi }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\varpi }_2\right)}{4}$

$\ge \frac{1}{\left({\varpi }_1-{\sigma }_1\right)\left({\varpi }_2-{\sigma }_2\right)}{\displaystyle {\int }_{{\sigma }_1}^{{\varpi }_1}}{\displaystyle {\int }_{{\sigma }_2}^{{\varpi }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa \text{ (1}\text{.2)}$

$\ge Ϝ\left(\frac{{\sigma }_1+{\varpi }_1}{2}\mathrm{,}\frac{{\sigma }_2+{\varpi }_2}{2}\right)\mathrm{.}$

The Hadamard-type inequality for s-convex functions in the second sense, defined on the coordinates of a rectangle in the plane ${ℝ}^2$ , was established by Alomari and M. Darus in [21].

Alomari and M. Darus established similar inequalities of Hadamard's type for s-convex functions defined on the coordinates in the first sense on a rectangle in the plane ${ℝ}^2$ [11]  Hadamard inequality for h-convex functions defined on the coordinates of a rectangle in the plane ${ℝ}^2$  was introduced by Amer Latif and M. W. Alomari in [22].

The Hermite-Hadamard Inequality spans a wide range of operator convex functions, giving rise to numerous intriguing inequalities within the dynamic field of matrix analysis. A natural progression from the classical Hermite-Hadamard Inequality to Hermitian matrices could entail a double inequality. This extension aims to capture the interplay between the inherent properties of Hermitian matrices and the principles underlying the Hermite-Hadamard Inequality, potentially yielding new insights and applications in matrix analysis.

The Hermite–Hadamard-Mercer type inequality is an extension of the classical Hermite–Hadamard inequality. It provides a relationship between the average value of a function over an interval and the function's integral. Specifically, it states that if a function is convex (or satisfies certain convexity conditions) on a given interval, then the average value of the function over that interval is greater than or equal to the value of the function at the midpoint of the interval. This inequality has various applications in mathematical analysis, optimization, and related fields. The literature regarding Hermite–Hadamard-Mercer inequality is as follows:

In 2003, Mercer authored a paper discussing a modification of Jensen's Inequality [23]. In 2006, Pe arić and their colleagues introduced a concept of Mercer-type Jensen inequality for operator convex functions, accompanied by various applications [24]. Niezgoda in 2009, worked on the generalization of Mercer's result on the convex functions [25]. Hermite–Hadamard-Mercer-type inequality was introduced by Kian, et al. in 2013 [26]. Hermite–Hadamard-Mercer Inequality for -convex functions are given by Xu, et al. in [27].

In mathematics, there's a crucial link between the value of a convex function evaluated at an integral and the integral of a convex function itself. This connection is formally termed Jensen's inequality, named after the Danish mathematician Johan Jensen, who formulated it in 1906. Jensen's inequality for convex functions holds a prominent place among the most celebrated inequalities in both mathematical and statistical realms. It serves as a foundational principle from which numerous other notable inequalities stem. Notably, Hölder's inequality and Minkowski's inequality emerge as special instances of Jensen's inequality for convex functions, highlighting its extensive applicability. Over time, a multitude of variations, refinements, and generalizations of Jensen's inequalities have been developed and extensively investigated, underscoring its enduring importance and versatility across diverse mathematical contexts. For more detail, one can be seen [28-32].

The outline of the article is structured as follows: In Section 2, we provide fundamental definitions and preliminary concepts to establish a solid foundation for our subsequent discussions. In Section 3, we demonstrate the Jensen-Mercer inequality and Hermite–Haamard–Mercer type inequalities for coordinated h-convex functions, contributing to the theoretical framework of our research. Section 4 presents numerical examples and computational analyses, offering empirical validation of the newly derived results and their practical significance. Finally, in Section 5, we present our conclusions, summarizing the key findings and implications of our study.

2. Preliminaries

In this section, we present some basic definitions and results which are required to establish the ongoing article.

Definition 1

[33] Let I be a convex subset of a real vector space and $Ϝ\mathrm{<mo>:</mo>}I\subset ℝ\to ℝ$  is said to be convex if

$\tau Ϝ\mathrm{<mo\; stretchy="false">(</mo>}\varkappa \mathrm{<mo\; stretchy="false">)</mo>}+\mathrm{<mo\; stretchy="false">(</mo>1}-\tau \mathrm{<mo\; stretchy="false">)</mo>}Ϝ\mathrm{<mo\; stretchy="false">(</mo>}\gamma \mathrm{<mo\; stretchy="false">)</mo>}\ge Ϝ\mathrm{<mo\; stretchy="false">(</mo>}\tau \varkappa +\mathrm{<mo\; stretchy="false">(</mo>1}-\tau \mathrm{<mo\; stretchy="false">)</mo>}\gamma \mathrm{<mo\; stretchy="false">)</mo>,}\text{ (2}\text{.1)}$

$\text{for all }\tau \in \mathrm{0,1<mo\; stretchy="false">]</mo>,}\text{ and }\varkappa \mathrm{,}\gamma \in I\mathrm{.}$

Definition 2

[4] A function  $Ϝ\mathrm{<mo>:</mo><mo\; stretchy="false">[</mo>0,}+\infty \mathrm{<mo\; stretchy="false">)</mo>}\to ℝ$ is said to be s-convex if

${\tau }^sϜ\mathrm{<mo\; stretchy="false">(</mo>}\varkappa \mathrm{<mo\; stretchy="false">)</mo>}+{\mathrm{<mo\; stretchy="false">(</mo>1}-\tau \mathrm{<mo\; stretchy="false">)</mo>}}^sϜ\mathrm{<mo\; stretchy="false">(</mo>}{\varpi }_1\mathrm{<mo\; stretchy="false">)</mo>}\ge Ϝ\left(\tau \varkappa +\mathrm{<mo\; stretchy="false">(</mo>1}-\tau \mathrm{<mo\; stretchy="false">)</mo>}{\varpi }_1\right)\mathrm{,}\text{ (2}\text{.2)}$

$\text{for all }\tau \in \mathrm{0,1<mo\; stretchy="false">]</mo>,}s\in \mathrm{<mo\; stretchy="false">(</mo>0,1<mo\; stretchy="false">]</mo>,}\text{ and }\varkappa \mathrm{,}{\varpi }_1\in \mathrm{0,}+\infty \mathrm{<mo\; stretchy="false">)</mo>.}$

Definition 3

Let $h\mathrm{<mo>:</mo>}\left(\mathrm{0,1}\right)\subseteq J\subseteq ℝ\to ℝ$  be a positive function. A function $Ϝ\mathrm{<mo>:</mo>}I\subseteq ℝ\to ℝ$ is said to be h-convex or that F is said to belong to the class $S\varkappa \left(h\mathrm{,}I\right)$ , if F is non-negative and for all $\varkappa \mathrm{,}\gamma \in I\in I$  and $\tau \in \left(\mathrm{0,1}\right)$ , we have

$h\left(\tau \right)Ϝ\mathrm{<mo\; stretchy="false">(</mo>}\varkappa \mathrm{<mo\; stretchy="false">)</mo>}+h\mathrm{<mo\; stretchy="false">(</mo>1}-\tau \mathrm{<mo\; stretchy="false">)</mo>}Ϝ\mathrm{<mo\; stretchy="false">(</mo>}\gamma \mathrm{<mo\; stretchy="false">)</mo>}\ge Ϝ\mathrm{<mo\; stretchy="false">(</mo>}\tau \varkappa +\mathrm{<mo\; stretchy="false">(</mo>1}-\tau \mathrm{<mo\; stretchy="false">)</mo>}\gamma \mathrm{<mo\; stretchy="false">)</mo>.}\text{ (2}\text{.3)}$

Definition 4

[9] A mapping $Ϝ\mathrm{<mo>:</mo>}\Delta \subset {ℝ}^2\to ℝ$ is convex on co-ordinates, if the following inequality holds:

$\tau Ϝ\left(\varkappa \mathrm{,}\gamma \right)+\left(1-\tau \right)Ϝ\left({\xi }_1\mathrm{,}{\eta }_1\right)\ge Ϝ\left(\tau \varkappa +\left(1-\tau \right){\xi }_1\mathrm{,}\tau \gamma +\left(1-\tau \right){\eta }_1\right)\mathrm{,}\text{ (2}\text{.4)}$

$\text{for all}\left(\varkappa \mathrm{,}\gamma \right)\mathrm{,}\left({\xi }_1\mathrm{,}{\eta }_1\right)\in \Delta \text{and }\tau \in \mathrm{0,1<mo\; stretchy="false">]</mo>,}$

Dragomir introduced a modification for convex functions on coordinates, referred to as coordinated convex functions [9,10] as follows: A function $Ϝ\mathrm{<mo>:</mo>}\Delta \subset {ℝ}^2\to ℝ$ is convex on the co-ordinates on Δ if the partial differentiable mappings ${Ϝ}_{\gamma }\mathrm{<mo>:</mo>}\left[{\sigma }_1\mathrm{,}{\varpi }_1\right]\to ℝ\mathrm{,}{Ϝ}_{\gamma }\left({\xi }_2\right)\mathrm{<mo>=</mo>}Ϝ\left({\xi }_2\mathrm{,}\gamma \right)$ and ${Ϝ}_{\varkappa }\mathrm{<mo>:</mo>}\left[{\sigma }_2\mathrm{,}{\varpi }_2\right]\to ℝ\mathrm{,}{Ϝ}_{\varkappa }\left({\eta }_2\right)\mathrm{<mo>=</mo>}Ϝ\left(\varkappa \mathrm{,}{\eta }_2\right)$  are convex for all $\varkappa \in \left[{\sigma }_1\mathrm{,}{\varpi }_1\right]\mathrm{,}\gamma \in \left[{\sigma }_2\mathrm{,}{\varpi }_2\right]\mathrm{.}$

A formal definition of coordinated convex functions can be expressed as follows:

Definition 5

[20] A mapping $Ϝ\mathrm{<mo>:</mo>}\Delta \subset {ℝ}^2\to ℝ$ is convex on co-ordinates, if the following inequality holds:

$\begin{array}{l}\theta \tau Ϝ\left(\varkappa \mathrm{,}\gamma \right)+\theta \left(1-\tau \right)Ϝ\left(\varkappa \mathrm{,}{\eta }_1\right)+\left(1-\theta \right)\tau Ϝ\left({\xi }_1\mathrm{,}\gamma \right)+\left(1-\tau \right)\left(1-\theta \right)Ϝ\left({\xi }_1\mathrm{,}{\eta }_1\right)\text{ (2}\text{.5)}\\ \ge Ϝ\left(\theta \varkappa +\left(1-\theta \right){\xi }_1\mathrm{,}\tau \gamma +\left(1-\tau \right){\eta }_1\right)\mathrm{,}\end{array}$

$\text{for all }\left(\varkappa \mathrm{,}\gamma \right)\mathrm{,}\left({\xi }_1\mathrm{,}{\eta }_1\right)\in \Delta \text{and }\theta \mathrm{,}\tau \in \left[\mathrm{0,1}\right]\mathrm{.}$

Definition 6

A mapping $Ϝ\mathrm{<mo>:</mo>}\Delta \subset {ℝ}^2\to ℝ$ is h-convex on co-ordinates, if the following inequality holds:

$\begin{array}{l}h\left(\theta \right)h\left(\tau \right)Ϝ\left(\varkappa \mathrm{,}\gamma \right)+h\left(\theta \right)h\left(1-\tau \right)Ϝ\left(\varkappa \mathrm{,}{\eta }_1\right)\\ +h\left(1-\theta \right)h\left(\tau \right)Ϝ\left({\xi }_1\mathrm{,}\gamma \right)+h\left(1-\tau \right)h\left(1-\theta \right)Ϝ\left({\xi }_1\mathrm{,}{\eta }_1\right)\\ \ge Ϝ\left(\theta \varkappa +\left(1-\theta \right){\xi }_1\mathrm{,}\tau \gamma +\left(1-\tau \right){\eta }_1\right)\mathrm{,}\end{array}$

$\text{for all}\left(\varkappa \mathrm{,}\gamma \right)\mathrm{,}\left({\xi }_1\mathrm{,}{\eta }_1\right)\in \Delta \text{ and}\theta \mathrm{,}\tau \in \left[\mathrm{0,1}\right]\mathrm{.}\text{ (2}\text{.6)}$

Definition 7

 [7] Let F be h-convex function defined on the real interval $\chi \subset ℝ\mathrm{.}$  If $\varkappa \mathrm{,}\gamma \mathrm{,}{\varkappa }_3\mathrm{,...,}{\varkappa }_n\in \chi$  and ${\xi }_1{}_1\mathrm{,}{\xi }_1{}_2\mathrm{,}{\xi }_1{}_3\mathrm{,...,}{\xi }_1{}_n\ge \mathrm{0,}$  also $h\mathrm{<mo>:</mo>}\zeta \subseteq \left(\mathrm{0,}\infty \right)\to {ℝ}^{+}$  be a supermultiplicative function then

${\displaystyle \sum _{i\mathrm{<mo>=</mo>1}}^n}h\left(\frac{{\xi }_i}{{\xi }_n}\right)Ϝ\mathrm{<mo\; stretchy="false">(</mo>}{\varkappa }_i\mathrm{<mo\; stretchy="false">)</mo>}\ge Ϝ\left(\frac{1}{{\xi }_1{}_n}{\displaystyle \sum _{i\mathrm{<mo>=</mo>1}}^n}{\xi }_i{\varkappa }_i\right)\mathrm{,}\text{ (2}\text{.7)}$

where ${\xi }_n\mathrm{<mo>=</mo>}{\displaystyle {\sum }_{i\mathrm{<mo>=</mo>1}}^n}{\xi }_i\mathrm{.}$

Definition 8

[34] Let $h\mathrm{<mo>:</mo>}\zeta \to {ℝ}^{+}$  be a supermultiplicative function Let $\varkappa \mathrm{,}\gamma \mathrm{,}{\varkappa }_3\mathrm{,...,}{\varkappa }_n\in \chi$ and $q_1\mathrm{,}{q}_2\mathrm{,}{q}_3\mathrm{,...,}{q}_n\in {ℝ}^{+}\mathrm{,}\left(n\ge 2\right)\mathrm{,}$  such that $Q_n\mathrm{<mo>=</mo>}{\displaystyle {\sum }_{i\mathrm{<mo>=</mo>1}}^n}{q}_i\text{ and }{\displaystyle {\sum }_{i\mathrm{<mo>=</mo>1}}^n}h\left(\frac{q_i}{Q_n}\right)\le 1.$  If F be h-convex function defined on the real interval $\chi \subset ℝ\mathrm{,}$  then for any finite positive increasing sequence ${\left({\varkappa }_k\right)}_{k\mathrm{<mo>=</mo>1}}^n\in \chi \mathrm{,}$  we have

$\begin{array}{l}Ϝ\left(\varkappa \right)+Ϝ\left({\varkappa }_n\right)-{\displaystyle \sum _{i\mathrm{<mo>=</mo>1}}^n}h\left(\frac{qi}{Q_n}\right)Ϝ\mathrm{<mo\; stretchy="false">(</mo>}{\varkappa }_i\mathrm{<mo\; stretchy="false">)</mo>}\text{ (2}\text{.8)}\\ \ge Ϝ\left(\varkappa +{\varkappa }_n-\frac{1}{Q_n}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}{q}_k{\xi }_k\right)\mathrm{.}\end{array}$

Definition 9

[35] This definition provided by Stromer, describes a function $g\mathrm{<mo>:</mo>}I\subset {ℝ}^{+}\to ℝ$  as a super-multiplicative if it satisfies the inequality

$g\mathrm{<mo\; stretchy="false">(</mo>}\alpha \mathrm{<mo\; stretchy="false">)</mo>}g\left(\beta \right)\le g\left(\alpha \beta \right)\mathrm{,}\text{ (2}\text{.9)}$

for all $\alpha \mathrm{,}\beta \in I\mathrm{.}$ Conversely, if the inequality is reversed, the function g is termed as sub-multiplicative.

Example 1

Consider the function $g\left(\varkappa \right)\mathrm{<mo>=</mo><mo\; stretchy="false">(</mo>}{\sigma }_1+\varkappa {\mathrm{<mo\; stretchy="false">)</mo>}}^{p-1}\mathrm{,}$  where $\varkappa \ge 0.$ If ${\sigma }_1\ge \mathrm{1,}$  then for $p\in \left(\mathrm{0,1}\right)$ the function g is super-multiplicative, it means the function g satisfies the inequality (2.9), on the other hand, p>1 the function g is sub-multiplicative.

3. Main results

In this section, we introduce Jensen-Mercer inequality and several Hermite–Hadamard-Mercer type inequalities tailored for coordinated h-convex functions.

Lemma 1

 Let $h\mathrm{<mo>:</mo>}J\subset {ℝ}^2\to ℝ$  is a non-negative supper multiplicative function, and $a\mathrm{,}c\mathrm{,}b\mathrm{,}e\in \left[\mathrm{0,1}\right]\mathrm{,}$  such that $h\left(a\right)+h\left(c\right)\le 1$  and $h\left(b\right)+h\left(e\right)\le 1.$  Then $Ϝ\mathrm{<mo>:</mo>}\Delta \subset {ℝ}^2\to ℝ$  is any co-ordinated h-convex function, and finite positive increasing sequences ${\left({\eta }_k\right)}_{k\mathrm{<mo>=</mo>1}}^n$  and ${\left({\xi }_k\right)}_{k\mathrm{<mo>=</mo>1}}^n\mathrm{.}$  Then,

$\begin{array}{l}Ϝ\left({\eta }_1+{\eta }_n-{\eta }_k\mathrm{,}{\xi }_1+{\xi }_n-{\xi }_k\right)\\ \le Ϝ\left({\eta }_1\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_1\mathrm{,}{\xi }_n\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_n\right)-Ϝ\left({\eta }_k\mathrm{,}{\xi }_k\right)\mathrm{,}\text{ (3}\text{.1)}\end{array}$

where $1\le k\le n\mathrm{.}$

Proof. Assume that $\mathrm{0<mo><</mo>}{\eta }_1\le {\eta }_2\le \mathrm{...}\le {\eta }_n$ and $\mathrm{0<mo><</mo>}{\xi }_1\le {\xi }_2\le \mathrm{...}\le {\xi }_n\mathrm{,}$ also $a\mathrm{,}c\mathrm{,}b\mathrm{,}e\in \left[\mathrm{0,1}\right]\mathrm{,}$ such that $h\left(a\right)+h\left(c\right)\le 1$ and $h\left(b\right)+h\left(e\right)\le 1.$ Let us write ${\gamma }_k\mathrm{<mo>=</mo>}{\eta }_1+{\eta }_n-{\eta }_k\mathrm{.}$ Then ${\eta }_1+{\eta }_n\mathrm{<mo>=</mo>}{\eta }_k+{\gamma }_k$ so that the pairs ${\eta }_1\mathrm{,}{\eta }_n$ and ${\eta }_k\mathrm{,}{\gamma }_k$ possess the same midpoint. Since that is the case there exists $a\mathrm{,}c\in \left[\mathrm{0,1}\right]\mathrm{,}$ such that

${\eta }_k\mathrm{<mo>=</mo>}a{\eta }_1+c{\eta }_n\mathrm{,}$

${\gamma }_k\mathrm{<mo>=</mo>}c{\eta }_1+a{\eta }_n\mathrm{.}$

Similarly, it can be written as ${\zeta }_k\mathrm{<mo>=</mo>}{\xi }_1+{\xi }_n-{\xi }_k\mathrm{.}$ Then ${\xi }_1+{\xi }_n\mathrm{<mo>=</mo>}{\xi }_k+{\eta }_k$ so that the pairs ${\xi }_1\mathrm{,}{\xi }_n$ and ${\xi }_k\mathrm{,}{\eta }_k$ share the same midpoint. Since that is the case there exists $b\mathrm{,}e\in \left[\mathrm{0,1}\right]\mathrm{,}$ such that

$\begin{array}{l}{\xi }_k\mathrm{<mo>=</mo>}b{\xi }_1+e{\xi }_n\mathrm{,}\\ {\zeta }_k\mathrm{<mo>=</mo>}e{\xi }_1+b{\xi }_n\mathrm{,}\end{array}$

$\text{where }s\mathrm{,}\tau \in \left[\mathrm{0,1}\right]\text{ and }1\le k\le n\mathrm{.}$

$\begin{array}{l}Ϝ\left({\gamma }_k\mathrm{,}{\zeta }_k\right)\mathrm{<mo>=</mo>}Ϝ\left(c{\eta }_1+a{\eta }_n\mathrm{,}e{\xi }_1+b{\xi }_n\right)\\ \le h\left(c\right)h\left(e\right)Ϝ\left({\eta }_1\mathrm{,}{\xi }_1\right)+h\left(c\right)h\left(b\right)Ϝ\left({\eta }_1\mathrm{,}{\xi }_n\right)\\ +h\left(a\right)h\left(e\right)Ϝ\left({\eta }_n\mathrm{,}{\xi }_1\right)+h\left(a\right)h\left(b\right)Ϝ\left({\eta }_n\mathrm{,}{\xi }_n\right)\mathrm{,}\text{ (3}\text{.2)}\end{array}$

$\begin{array}{l}Ϝ\left({\eta }_k\mathrm{,}{\xi }_k\right)\mathrm{<mo>=</mo>}Ϝ\left(a{\eta }_1+c{\eta }_n\mathrm{,}b{\xi }_1+e{\xi }_n\right)\\ \le h\left(a\right)h\left(b\right)Ϝ\left({\eta }_1\mathrm{,}{\xi }_1\right)+h\left(a\right)h\left(e\right)Ϝ\left({\eta }_1\mathrm{,}{\xi }_n\right)\\ +h\left(c\right)h\left(b\right)Ϝ\left({\eta }_n\mathrm{,}{\xi }_1\right)+h\left(c\right)h\left(e\right)Ϝ\left({\eta }_n\mathrm{,}{\xi }_n\right)\mathrm{.}\text{ (3}\text{.3)}\end{array}$

By Jensen inequality for co-ordinated h-convex functions and using (3.3)

$Ϝ\left({\gamma }_k\mathrm{,}{\zeta }_k\right)$

$\le h\left(c\right)h\left(e\right)Ϝ\left({\eta }_1\mathrm{,}{\xi }_1\right)+h\left(c\right)h\left(b\right)Ϝ\left({\eta }_1\mathrm{,}{\xi }_n\right)+h\left(a\right)h\left(e\right)Ϝ\left({\eta }_n\mathrm{,}{\xi }_1\right)+h\left(a\right)h\left(b\right)Ϝ\left({\eta }_n\mathrm{,}{\xi }_n\right)$

$\le \left(1-h\left(a\right)\right)\left(1-h\left(b\right)\right)Ϝ\left({\eta }_1\mathrm{,}{\xi }_1\right)+\left(1-h\left(a\right)\right)\left(1-h\left(e\right)\right)Ϝ\left({\eta }_1\mathrm{,}{\xi }_n\right)$

$+\left(1-h\left(c\right)\right)\left(1-h\left(b\right)\right)Ϝ\left({\eta }_n\mathrm{,}{\xi }_1\right)+\left(1-h\left(c\right)\right)\left(1-h\left(e\right)\right)Ϝ\left({\eta }_n\mathrm{,}{\xi }_n\right)$

$\mathrm{<mo>=</mo>}Ϝ\left({\eta }_1\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_1\mathrm{,}{\xi }_n\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_n\right)$

$-[\left(h\left(a\right)+h\left(b\right)-h\left(a\right)h\left(b\right)\right)Ϝ\left({\eta }_1\mathrm{,}{\xi }_1\right)+\left(h\left(a\right)+h\left(e\right)-h\left(a\right)h\left(e\right)\right)Ϝ\left({\eta }_1\mathrm{,}{\xi }_n\right)$

$+\left(h\left(c\right)+h\left(b\right)-h\left(c\right)h\left(b\right)\right)Ϝ\left({\eta }_n\mathrm{,}{\xi }_1\right)+\left(h\left(c\right)+h\left(e\right)-h\left(c\right)h\left(e\right)\right)Ϝ\left({\eta }_n\mathrm{,}{\xi }_n\right)]$

$\le Ϝ\left({\eta }_1\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_1\mathrm{,}{\xi }_n\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_n\right)$

$-\left[h\left(a\right)h\left(b\right)Ϝ\left({\eta }_1\mathrm{,}{\xi }_1\right)+h\left(a\right)h\left(e\right)Ϝ\left({\eta }_1\mathrm{,}{\xi }_n\right)+h\left(c\right)h\left(b\right)Ϝ\left({\eta }_n\mathrm{,}{\xi }_1\right)+h\left(c\right)h\left(e\right)Ϝ\left({\eta }_n\mathrm{,}{\xi }_n\right)\right]$

$\le Ϝ\left({\eta }_1\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_1\mathrm{,}{\xi }_n\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_n\right)-Ϝ\left({\eta }_k\mathrm{,}{\xi }_k\right)\mathrm{,}$

where $h\left(a\right)+h\left(b\right)-h\left(a\right)h\left(b\right)\ge h\left(a\right)h\left(b\right)\mathrm{,}h\left(a\right)+h\left(e\right)-h\left(a\right)h\left(e\right)\ge h\left(a\right)h\left(e\right)\mathrm{,}h\left(c\right)+h\left(b\right)-h\left(c\right)h\left(b\right)\ge h\left(c\right)h\left(b\right)\mathrm{,}$ and $h\left(c\right)+h\left(e\right)-h\left(c\right)h\left(e\right)\ge h\left(c\right)h\left(e\right)$ for $a\mathrm{,}c\mathrm{,}b\mathrm{,}e\in \left[\mathrm{0,1}\right]$ .

Hence, we have

$Ϝ\left({\eta }_1+{\eta }_n-{\eta }_k\mathrm{,}{\xi }_1+{\xi }_n-{\xi }_k\right)$

$\le Ϝ\left({\eta }_1\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_1\mathrm{,}{\xi }_n\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_n\right)-Ϝ\left({\eta }_k\mathrm{,}{\xi }_k\right)\mathrm{.}$

The proof of Lemma 1 is completed.

Theorem 2

 Let $z_1\mathrm{,}{z}_2\mathrm{,}{z}_3\mathrm{,...,}{z}_n\in ℝ$  and $q_1\mathrm{,}{q}_2\mathrm{,}{q}_3\mathrm{,...,}{q}_n\in ℝ$ , $\left(n\ge 2\right)\mathrm{,}$  such that ${\mathbb{Z}}_n\mathrm{<mo>=</mo>}{\displaystyle {\sum }_{k\mathrm{<mo>=</mo>1}}^n}{z}_k$  and ${\mathbb{Q}}_n\mathrm{<mo>=</mo>}{\displaystyle {\sum }_{k\mathrm{<mo>=</mo>1}}^n}{q}_k$ . Also, assume that $h\mathrm{<mo>:</mo>}J\subset {ℝ}^2\to ℝ$  is a non-negative supper multiplicative function with ${\displaystyle {\sum }_{k\mathrm{<mo>=</mo>1}}^n}h\left(\frac{z_k}{{\mathbb{Z}}_n}\right)\le 1$  and ${\displaystyle {\sum }_{k\mathrm{<mo>=</mo>1}}^n}h\left(\frac{q_k}{{\mathbb{Q}}_n}\right)\le 1$  respectively. If the function $Ϝ\mathrm{<mo>:</mo>}\Delta \subset {ℝ}^2\to ℝ$  is co-ordinated h-convex on $\Delta \mathrm{<mo>=</mo>}\left[{\eta }_1\mathrm{,}{\eta }_n\right]\times \left[{\xi }_1\mathrm{,}{\xi }_n\right]$ then for any finite positive sequences ${\left({\eta }_k\right)}_{k\mathrm{<mo>=</mo>1}}^n$  and ${\left({\xi }_k\right)}_{k\mathrm{<mo>=</mo>1}}^n$  from $\Delta \mathrm{.}$  Then

$Ϝ\left({\eta }_1+{\eta }_n-\frac{1}{{\mathbb{Z}}_n}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}{z}_k{\eta }_k\mathrm{,}{\xi }_1+{\xi }_n-\frac{1}{{\mathbb{Q}}_n}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}{q}_k{\xi }_k\right)$

$\le Ϝ\left({\eta }_1\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_1\mathrm{,}{\xi }_n\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_n\right)$

$-{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}h\left(\frac{z_k}{{\mathbb{Z}}_n}\right){\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}h\left(\frac{q_k}{{\mathbb{Q}}_n}\right)Ϝ\left({\eta }_k\mathrm{,}{\xi }_k\right)\mathrm{.}\text{ (3}\text{.4)}$

Proof. Since $\frac{1}{{\mathbb{Z}}_n}{\displaystyle {\sum }_{k\mathrm{<mo>=</mo>1}}^n}{z}_k\mathrm{<mo>=</mo>1}$ and $\frac{1}{{\mathbb{Q}}_n}{\displaystyle {\sum }_{k\mathrm{<mo>=</mo>1}}^n}{q}_k\mathrm{<mo>=</mo>1,}$ we have:

$Ϝ\left({\eta }_1+{\eta }_n-\frac{1}{{\mathbb{Z}}_n}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}{z}_k{\eta }_k\mathrm{,}{\xi }_1+{\xi }_n-\frac{1}{{\mathbb{Q}}_n}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}{q}_k{\xi }_k\right)$

$\mathrm{<mo>=</mo>}Ϝ\left({\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}\frac{z_k}{{\mathbb{Z}}_n}\left({\eta }_1+{\eta }_n-{\eta }_k\right)\mathrm{,}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}\frac{q_k}{{\mathbb{Q}}_n}\left({\xi }_1+{\xi }_n-{\xi }_k\right)\right)$

$\le {\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}h\left(\frac{z_k}{{\mathbb{Z}}_n}\right){\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}h\left(\frac{q_k}{{\mathbb{Q}}_n}\right)Ϝ\left({\eta }_1+{\eta }_n-{\eta }_k\mathrm{,}{\xi }_1+{\xi }_n-{\xi }_k\right)$

$\le {\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}h\left(\frac{z_k}{{\mathbb{Z}}_n}\right){\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}h\left(\frac{q_k}{{\mathbb{Q}}_n}\right)\left[Ϝ\left({\eta }_1\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_1\mathrm{,}{\xi }_n\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_n\right)-Ϝ\left({\eta }_k\mathrm{,}{\xi }_k\right)\right]$

$\mathrm{<mo>=</mo>}Ϝ\left({\eta }_1\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_1\mathrm{,}{\xi }_n\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_1\right)+Ϝ\left({\eta }_n\mathrm{,}{\xi }_n\right)-{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}h\left(\frac{z_k}{{\mathbb{Z}}_n}\right){\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^n}h\left(\frac{q_k}{{\mathbb{Q}}_n}\right)Ϝ\left({\eta }_k\mathrm{,}{\xi }_k\right)\mathrm{.}$

Hence the proof of Theorem 2 is completed.

Theorem 3

Suppose that $Ϝ\mathrm{<mo>:</mo>}\Delta \mathrm{<mo>=</mo>}\left[{\sigma }_1\mathrm{,}{\varpi }_1\right]\times \left[{\sigma }_2\mathrm{,}{\varpi }_2\right]\subseteq {ℝ}^2\to ℝ$ be an h-convex function on co-ordinates on Δ and let $Ϝ\in L_2\left(\Delta \right)$  and $h\in L_1\left(\left[\mathrm{0,1}\right]\right)$ . Then one has the inequalities:

$\frac{1}{4{\left(h\left(\frac{1}{2}\right)\right)}^2}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)$

$\le \frac{1}{\left({\eta }_1-{\xi }_1\right)\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa$

$\le 4\left[Ϝ\left({\sigma }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\sigma }_1\mathrm{,}{\varpi }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\varpi }_2\right)\right]\times {\left({\displaystyle {\int }_0^1}h\left(\tau \right)d\tau \right)}^2$

$-\left[Ϝ\left({\eta }_1\mathrm{,}{\xi }_2\right)+Ϝ\left({\eta }_1\mathrm{,}{\eta }_2\right)+Ϝ\left({\xi }_1\mathrm{,}{\xi }_2\right)+Ϝ\left({\xi }_1\mathrm{,}{\eta }_2\right)\right]\times {\left({\displaystyle {\int }_0^1}h\left(\tau \right)d\tau \right)}^2\mathrm{,}\text{ (3}\text{.5)}$

where ${\xi }_1\mathrm{,}{\eta }_1\in \left[{\sigma }_1\mathrm{,}{\varpi }_1\right]$ and ${\xi }_2\mathrm{,}{\eta }_2\in \left[{\sigma }_2\mathrm{,}{\varpi }_2\right]\mathrm{.}$

Proof. Since $Ϝ\mathrm{<mo>:</mo>}\Delta \to ℝ$ is h-convex function on co-ordinates also ${\Psi }_{\varkappa }\mathrm{<mo>:</mo>}\left[{\sigma }_2\mathrm{,}{\varpi }_2\right]\to ℝ\mathrm{,}{\Psi }_{\varkappa }\left(\gamma \right)\mathrm{<mo>=</mo>}Ϝ\left(\varkappa \mathrm{,}\gamma \right)\mathrm{,}$ is h-convex on $\left[{\sigma }_2\mathrm{,}{\varpi }_2\right]\mathrm{,}$ for all $\varkappa \in \left[{\sigma }_1\mathrm{,}{\varpi }_1\right]\mathrm{.}$ Then by Hermite–Hadamard-Mercer Inequality for h-convex functions

$\frac{1}{2h\left(\frac{1}{2}\right)}{\Psi }_{\varkappa }\left({\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)$

$\le \frac{1}{\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}{\Psi }_{\varkappa }\left(\gamma \right)d\gamma \le \left[{\Psi }_{\varkappa }\left({\sigma }_2+{\varpi }_2-{\xi }_2\right)+{\Psi }_{\varkappa }\left({\sigma }_2+{\varpi }_2-{\eta }_2\right)\right]$

$\times \left({\displaystyle {\int }_0^1}h\left(\tau \right)d\tau \right)\mathrm{,}$

i.e.

$\frac{1}{2h\left(\frac{1}{2}\right)}Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)$

$\le \frac{1}{\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma$

$\le \left[Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-{\xi }_2\right)+Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-{\eta }_2\right)\right]\times \left({\displaystyle {\int }_0^1}h\left(\tau \right)d\tau \right)\mathrm{.}$

Integrating the above inequality with respect to $\varkappa$ , we get

$\frac{1}{2h\left(\frac{1}{2}\right)\left({\eta }_1-{\xi }_1\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)d\varkappa$

$\le \frac{1}{\left({\eta }_1-{\xi }_1\right)\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa$

$\le [\frac{1}{\left({\eta }_1-{\xi }_1\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-{\xi }_2\right)d\varkappa$

$+\frac{1}{\left({\eta }_1-{\xi }_1\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-{\eta }_2\right)d\varkappa ]\times \left({\displaystyle {\int }_0^1}h\left(\tau \right)d\tau \right)\mathrm{.}\text{ (3}\text{.6)}$

Similarly, for the mapping ${\Psi }_{\gamma }\mathrm{<mo>:</mo>}\left[{\sigma }_1\mathrm{,}{\varpi }_1\right]\to ℝ\mathrm{,}{\Psi }_{\gamma }\left(\varkappa \right)\mathrm{<mo>=</mo>}Ϝ\left(\varkappa \mathrm{,}\gamma \right)\mathrm{,}$ we get

$\frac{1}{2h\left(\frac{1}{2}\right)\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}\gamma \right)d\gamma$

$\le \frac{1}{\left({\eta }_1-{\xi }_1\right)\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa$

$\le [\frac{1}{\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left({\sigma }_1+{\varpi }_1-{\eta }_1\mathrm{,}\gamma \right)d\gamma$

$+\frac{1}{\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left({\sigma }_1+{\varpi }_1-{\xi }_1\mathrm{,}\gamma \right)d\gamma ]\times \left({\displaystyle {\int }_0^1}h\left(\tau \right)d\tau \right)\mathrm{.}\text{ (3}\text{.7)}$

By adding the inequalities (3.6) and (3.7), we get

$\frac{1}{4h\left(\frac{1}{2}\right)}[\frac{1}{\left({\eta }_1-{\xi }_1\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)d\varkappa$

$+\frac{1}{\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}\gamma \right)d\gamma ]$

$\le \frac{1}{\left({\eta }_1-{\xi }_1\right)\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa$

$\le \frac{1}{2}\{[\frac{1}{\left({\eta }_1-{\xi }_1\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-{\xi }_2\right)d\varkappa$

$+\frac{1}{\left({\eta }_1-{\xi }_1\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-{\eta }_2\right)d\varkappa$

$+\frac{1}{\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left({\sigma }_1+{\varpi }_1-{\eta }_1\mathrm{,}\gamma \right)d\gamma$

$+\frac{1}{\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left({\sigma }_1+{\varpi }_1-{\xi }_1\mathrm{,}\gamma \right)d\gamma ]\}\times \left({\displaystyle {\int }_0^1}h\left(\tau \right)d\tau \right)\mathrm{.}\text{ (3}\text{.8)}$

Now by Hadamard's Mercer inequality for h-convex functions, we have:

$\frac{1}{2h\left(\frac{1}{2}\right)}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)$

$\le \frac{1}{\left({\eta }_1-{\xi }_1\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)d\varkappa \mathrm{,}$

$\frac{1}{2h\left(\frac{1}{2}\right)}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)$

$\le \frac{1}{\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}\gamma \right)d\gamma \mathrm{.}$

Adding these inequalities, we have:

$\frac{1}{h\left(\frac{1}{2}\right)}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)$

$\le \frac{1}{\left({\eta }_1-{\xi }_1\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)d\varkappa$

$+\frac{1}{\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}\gamma \right)d\gamma \mathrm{.}$

By dividing both sides of the above inequality $4h\left(\frac{1}{2}\right)\mathrm{,}$ we get

$\frac{1}{4{\left(h\left(\frac{1}{2}\right)\right)}^2}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)$

$\le \frac{1}{4h\left(\frac{1}{2}\right)}[\frac{1}{\left({\eta }_1-{\xi }_1\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)d\varkappa$

$+\frac{1}{\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}\gamma \right)d\gamma ]\mathrm{.}\text{ (3}\text{.9)}$

Finally, by the inequality (3.8), we get:

$\frac{1}{\left({\eta }_1-{\xi }_1\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-{\xi }_2\right)d\varkappa$

$\le \left[Ϝ\left({\sigma }_1+{\varpi }_1-{\eta }_1\mathrm{,}{\sigma }_2+{\varpi }_2-{\xi }_2\right)+Ϝ\left({\sigma }_1+{\varpi }_1-{\xi }_1\mathrm{,}{\sigma }_2+{\varpi }_2-{\xi }_2\right)\right]\left({\displaystyle {\int }_0^1}h\left(\tau \right)d\tau \right)\mathrm{,}$

$\frac{1}{\left({\eta }_1-{\xi }_1\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-{\eta }_2\right)d\varkappa$

$\le \left[Ϝ\left({\sigma }_1+{\varpi }_1-{\eta }_1\mathrm{,}{\sigma }_2+{\varpi }_2-{\eta }_2\right)+Ϝ\left({\sigma }_1+{\varpi }_1-{\xi }_1\mathrm{,}{\sigma }_2+{\varpi }_2-{\eta }_2\right)\right]\left({\displaystyle {\int }_0^1}h\left(\tau \right)d\tau \right)\mathrm{,}$

$\frac{1}{\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left({\sigma }_1+{\varpi }_1-{\eta }_1\mathrm{,}\gamma \right)d\gamma$

$\le \left[Ϝ\left({\sigma }_1+{\varpi }_1-{\eta }_1\mathrm{,}{\sigma }_2+{\varpi }_2-{\xi }_2\right)+Ϝ\left({\sigma }_1+{\varpi }_1-{\eta }_1\mathrm{,}{\sigma }_2+{\varpi }_2-{\eta }_2\right)\right]\left({\displaystyle {\int }_0^1}h\left(\tau \right)d\tau \right)\mathrm{,}$

$\frac{1}{\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left({\sigma }_1+{\varpi }_1-{\xi }_1\mathrm{,}\gamma \right)d\gamma$

$\le \left[Ϝ\left({\sigma }_1+{\varpi }_1-{\xi }_1\mathrm{,}{\sigma }_2+{\varpi }_2-{\xi }_2\right)+Ϝ\left({\sigma }_1+{\varpi }_1-{\xi }_1\mathrm{,}{\sigma }_2+{\varpi }_2-{\eta }_2\right)\right]\left({\displaystyle {\int }_0^1}h\left(\tau \right)d\tau \right)\mathrm{.}$

Adding the above inequalities, we get

$\frac{1}{2}[\frac{1}{\left({\eta }_1-{\xi }_1\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-{\xi }_2\right)d\varkappa$

$+\frac{1}{\left({\eta }_1-{\xi }_1\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}Ϝ\left(\varkappa \mathrm{,}{\sigma }_2+{\varpi }_2-{\eta }_2\right)d\varkappa$

$+\frac{1}{\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left({\sigma }_1+{\varpi }_1-{\eta }_1\mathrm{,}\gamma \right)d\gamma$

$+\frac{1}{\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left({\sigma }_1+{\varpi }_1-{\xi }_1\mathrm{,}\gamma \right)d\gamma ]$

$\le [Ϝ\left({\sigma }_1+{\varpi }_1-{\eta }_1\mathrm{,}{\sigma }_2+{\varpi }_2-{\xi }_2\right)+Ϝ\left({\sigma }_1+{\varpi }_1-{\xi }_1\mathrm{,}{\sigma }_2+{\varpi }_2-{\xi }_2\right)$

$+Ϝ\left({\sigma }_1+{\varpi }_1-{\eta }_1\mathrm{,}{\sigma }_2+{\varpi }_2-{\eta }_2\right)+Ϝ\left({\sigma }_1+{\varpi }_1-{\xi }_1\mathrm{,}{\sigma }_2+{\varpi }_2-{\eta }_2\right)]$

$\times {\left({\displaystyle {\int }_0^1}h\left(\tau \right)d\tau \right)}^2\mathrm{.}\text{ (3}\text{.10)}$

From (3.6)-(3.10), and by using Jensen Mercer inequality for co-ordinated h-convex functions, we get (3.5). The proof of Theorem 3 is completed.

Corollary 1

If we replace $Ϝ\left(\tau \right)\mathrm{<mo>=</mo>}{\tau }^s$  in Theorem 3, we get the inequalities:

$4^{s-1}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)$

$\le \frac{1}{\left({\eta }_1-{\xi }_1\right)\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa$

$\le 4\left[\frac{Ϝ\left({\sigma }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\sigma }_1\mathrm{,}{\varpi }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\varpi }_2\right)}{{\left(s+1\right)}^2}\right]$

$-\left[\frac{Ϝ\left({\eta }_1\mathrm{,}{\xi }_2\right)+Ϝ\left({\eta }_1\mathrm{,}{\eta }_2\right)+Ϝ\left({\xi }_1\mathrm{,}{\xi }_2\right)+Ϝ\left({\xi }_1\mathrm{,}{\eta }_2\right)}{{\left(s+1\right)}^2}\right]\mathrm{.}\text{ (3}\text{.11)}$

Remark 1

If we replace $Ϝ\left(\tau \right)\mathrm{<mo>=</mo>}\tau$  in Theorem 3, we get the inequalities,

$Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)$

$\le \frac{1}{\left({\eta }_1-{\xi }_1\right)\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa$

$\le Ϝ\left({\sigma }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\sigma }_1\mathrm{,}{\varpi }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\varpi }_2\right)$

$-\left[\frac{Ϝ\left({\eta }_1\mathrm{,}{\xi }_2\right)+Ϝ\left({\eta }_1\mathrm{,}{\eta }_2\right)+Ϝ\left({\xi }_1\mathrm{,}{\xi }_2\right)+Ϝ\left({\xi }_1\mathrm{,}{\eta }_2\right)}{4}\right]\mathrm{,}\text{ (3}\text{.12)}$

which are already proved by Toseef, et al.

Remark 2

If we replace $Ϝ\left(\tau \right)\mathrm{<mo>=</mo>}\tau$ , and ${\sigma }_1\mathrm{<mo>=</mo>}{\xi }_1\mathrm{,}{\varpi }_1\mathrm{<mo>=</mo>}{\eta }_1\mathrm{,}{\sigma }_2\mathrm{<mo>=</mo>}{\xi }_2\mathrm{,}$  and ${\varpi }_2\mathrm{<mo>=</mo>}{\eta }_2\mathrm{,}$  in Theorem 3, we get the inequalities,

$Ϝ\left(\frac{{\sigma }_1+{\varpi }_1}{2}\mathrm{,}\frac{{\sigma }_2+{\varpi }_2}{2}\right)$

$\le \frac{1}{\left({\varpi }_1-{\sigma }_1\right)\left({\varpi }_2-{\sigma }_2\right)}{\displaystyle {\int }_{{\sigma }_1}^{{\varpi }_1}}{\displaystyle {\int }_{{\sigma }_2}^{{\varpi }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa$

$\le \frac{Ϝ\left({\sigma }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\sigma }_1\mathrm{,}{\varpi }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\varpi }_2\right)}{4}\mathrm{,}\text{ (3}\text{.13)}$

which are already proved by Dragomir in [8].

Remark 3

If we replace $Ϝ\left(\tau \right)\mathrm{<mo>=</mo>}\frac{1}{\tau }$ , and ${\sigma }_1\mathrm{<mo>=</mo>}{\xi }_1\mathrm{,}{\varpi }_1\mathrm{<mo>=</mo>}{\eta }_1\mathrm{,}{\sigma }_2\mathrm{<mo>=</mo>}{\xi }_2\mathrm{,}$  and ${\varpi }_2\mathrm{<mo>=</mo>}{\eta }_2\mathrm{,}$  in Theorem 3, we get the inequality:

$Ϝ\left(\frac{{\sigma }_1+{\varpi }_1}{2}\mathrm{,}\frac{{\sigma }_2+{\varpi }_2}{2}\right)$

$\le \frac{16}{\left({\varpi }_1-{\sigma }_1\right)\left({\varpi }_2-{\sigma }_2\right)}{\displaystyle {\int }_{{\sigma }_1}^{{\varpi }_1}}{\displaystyle {\int }_{{\sigma }_2}^{{\varpi }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa \mathrm{.}\text{ (3}\text{.14)}$

Remark 4

If we replace ${\sigma }_1\mathrm{<mo>=</mo>}{\xi }_1\mathrm{,}{\varpi }_1\mathrm{<mo>=</mo>}{\eta }_1\mathrm{,}{\sigma }_2\mathrm{<mo>=</mo>}{\xi }_2\mathrm{,}$  and ${\varpi }_2\mathrm{<mo>=</mo>}{\eta }_2\mathrm{,}$  in Theorem 3, we get the inequalities,

$\frac{1}{4{\left(h\left(\frac{1}{2}\right)\right)}^2}Ϝ\left(\frac{{\sigma }_1+{\varpi }_1}{2}\mathrm{,}\frac{{\sigma }_2+{\varpi }_2}{2}\right)$

$\le \frac{1}{\left({\varpi }_1-{\sigma }_1\right)\left({\varpi }_2-{\sigma }_2\right)}{\displaystyle {\int }_{{\sigma }_1}^{{\varpi }_1}}{\displaystyle {\int }_{{\sigma }_2}^{{\varpi }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa$

$\le \left[Ϝ\left({\sigma }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\sigma }_1\mathrm{,}{\varpi }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\varpi }_2\right)\right]{\left({\displaystyle {\int }_0^1}h\left(\tau \right)d\tau \right)}^2\mathrm{,}\text{ (3}\text{.15)}$

which are already proved by Alomari and Latif in [21].

4. Numerical examples and computational analysis

In this section, we give numerical examples and computational analysis of newly derived inequalities.

Example 2

$Ϝ\left(\varkappa \mathrm{,}\gamma \right)\mathrm{<mo>=</mo>}{\left(\varkappa -1\right)}^{2s}{\left(\gamma -1\right)}^{2s}$  is h-the convex function on $\left[\mathrm{2,10}\right]\times \left[\mathrm{2,10}\right]\subset \mathrm{0,}\infty \mathrm{<mo\; stretchy="false">)</mo>}\times \mathrm{0,}\infty \mathrm{<mo\; stretchy="false">)</mo>,}s\in \left(0.1\right)$  then there are three cases $\text{(i) }h\left(\tau \right)\mathrm{<mo>=</mo>}{\tau }^s\mathrm{,}\text{(ii) }h\left(\tau \right)\mathrm{<mo>=</mo>}\tau \mathrm{,}\text{(iii) }h\left(\tau \right)\mathrm{<mo>=</mo>}\frac{1}{\tau }\mathrm{.}$

In the first case: $h\left(\tau \right)\mathrm{<mo>=</mo>}{\tau }^s$ , $s\mathrm{<mo>=</mo>0.1}$

$4^{s-1}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)$

${\mathrm{<mo>=</mo>4}}^{s-1}{\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}-1\right)}^{2s}{\left({\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}-1\right)}^{2s}$

${\mathrm{<mo>=</mo>4}}^{0.1-1}{\left(2+10-\frac{3+7}{2}-1\right)}^{0.2}{\left(2+10-\frac{3+7}{2}-1\right)}^{0.2}$

$\mathrm{<mo>=</mo>0.5880,}$ (4.1)

$\frac{1}{\left({\eta }_1-{\xi }_1\right)\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa \mathrm{<mo>=</mo>2.0352,}\text{ (4}\text{.2)}$

$4\left[\frac{Ϝ\left({\sigma }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\sigma }_1\mathrm{,}{\varpi }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\varpi }_2\right)}{{\left(s+1\right)}^2}\right]$

$-\left[\frac{Ϝ\left({\eta }_1\mathrm{,}{\xi }_2\right)+Ϝ\left({\eta }_1\mathrm{,}{\eta }_2\right)+Ϝ\left({\xi }_1\mathrm{,}{\xi }_2\right)+Ϝ\left({\xi }_1\mathrm{,}{\eta }_2\right)}{{\left(s+1\right)}^2}\right]$

$\mathrm{<mo>=</mo>16.0273.}$ (4.3)

In the second case: $h\left(\tau \right)\mathrm{<mo>=</mo>}\tau$

$Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)$

$\mathrm{<mo>=</mo>}{\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}-1\right)}^2{\left({\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}-1\right)}^2$

$\mathrm{<mo>=</mo>}{\left(2+10-\frac{3+7}{2}-1\right)}^2{\left(2+10-\frac{3+7}{2}-1\right)}^2$

$\mathrm{<mo>=</mo>1296,}$ (4.3)

$\frac{1}{\left({\eta }_1-{\xi }_1\right)\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa \mathrm{<mo>=</mo>1393.778,}\text{ (4}\text{.4)}$

$Ϝ\left({\sigma }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\sigma }_1\mathrm{,}{\varpi }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\varpi }_2\right)$

$-\left[\frac{Ϝ\left({\eta }_1\mathrm{,}{\xi }_2\right)+Ϝ\left({\eta }_1\mathrm{,}{\eta }_2\right)+Ϝ\left({\xi }_1\mathrm{,}{\xi }_2\right)+Ϝ\left({\xi }_1\mathrm{,}{\eta }_2\right)}{4}\right]$

$\mathrm{<mo>=</mo>6324.0.}$ (4.5)

In the third case: $h\left(\tau \right)\mathrm{<mo>=</mo>}\frac{1}{\tau }$

$\frac{1}{16}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)\mathrm{<mo>=</mo>81,}$

$\frac{1}{\left({\eta }_1-{\xi }_1\right)\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa \mathrm{<mo>=</mo>1393.778.}$

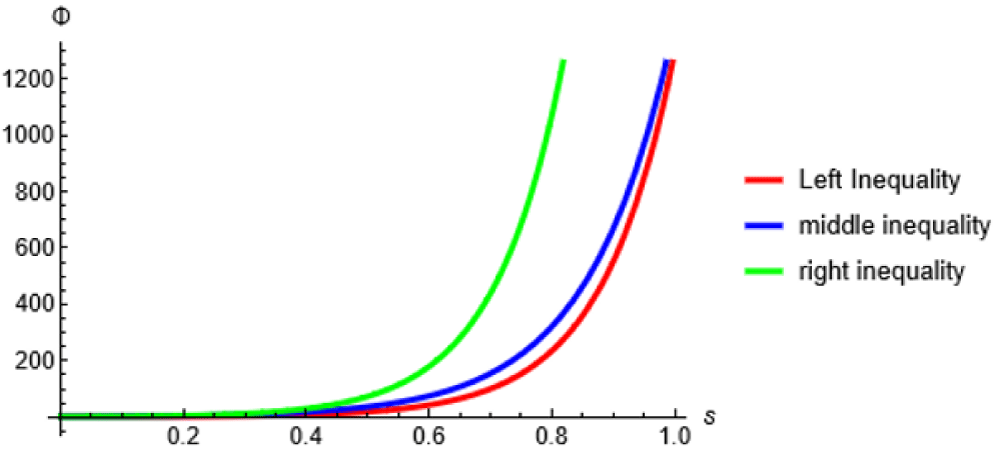
From inequalities (4.1)-(4.6), Table 1, and Graph we can conclude that inequalities of Theorem 3 are better when $s\to 0$ and worse when $s\to 1.$

Example 3

$Ϝ\left(\varkappa \mathrm{,}\gamma \right)\mathrm{<mo>=</mo>}{e}^{s\varkappa \gamma }$  is h-the convex function on $\left[\mathrm{2,10}\right]\times \left[\mathrm{2,10}\right]\subset \mathrm{0,}\infty \mathrm{<mo\; stretchy="false">)</mo>}\times \mathrm{0,}\infty \mathrm{<mo\; stretchy="false">)</mo>,}s\in \left(0.1\right)$  then there are three cases $\left(i\right)h\left(\tau \right)\mathrm{<mo>=</mo>}{\tau }^s\mathrm{,}\left(ii\right)h\left(\tau \right)\mathrm{<mo>=</mo>}\tau \mathrm{,}\left(iii\right)h\left(\tau \right)\mathrm{<mo>=</mo>}\frac{1}{\tau }\mathrm{.}$

In the first case: $h\left(\tau \right)\mathrm{<mo>=</mo>}{\tau }^s$ , $s\mathrm{<mo>=</mo>0.1}$

$4^{s-1}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)$

${\mathrm{<mo>=</mo>4}}^{s-1}\times e^{s\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\right)\left({\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)}$

${\mathrm{<mo>=</mo>4}}^{0.1-1}\times e^{0.1\left(2+10-\frac{3+7}{2}\right)\left(2+10-\frac{3+7}{2}\right)}$

$\mathrm{<mo>=</mo>38.5646,}$ (4.7)

$\frac{1}{\left({\eta }_1-{\xi }_1\right)\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa \mathrm{<mo>=</mo>269.08,}\text{ (4}\text{.8)}$

$4\left[\frac{Ϝ\left({\sigma }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\sigma }_1\mathrm{,}{\varpi }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\varpi }_2\right)}{{\left(s+1\right)}^2}\right]$

$-\left[\frac{Ϝ\left({\eta }_1\mathrm{,}{\xi }_2\right)+Ϝ\left({\eta }_1\mathrm{,}{\eta }_2\right)+Ϝ\left({\xi }_1\mathrm{,}{\xi }_2\right)+Ϝ\left({\xi }_1\mathrm{,}{\eta }_2\right)}{{\left(s+1\right)}^2}\right]$

$\mathrm{<mo>=</mo>72742.}$ (4.9)

In the second case: $h\left(\tau \right)\mathrm{<mo>=</mo>}\tau$

$Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)$

${\mathrm{<mo>=</mo>4}}^0\times e^{\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\right)\left({\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)}$

$\mathrm{<mo>=</mo>}{e}^{\left(2+10-\frac{3+7}{2}\right)\left(2+10-\frac{3+7}{2}\right)}$

$\mathrm{<mo>=</mo>1.1524}\times {10}^{21}\mathrm{,}$ (4.10)

$\frac{1}{\left({\eta }_1-{\xi }_1\right)\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa \mathrm{<mo>=</mo>5.3422}\times {10}^{31}\mathrm{,}\text{ (4}\text{.11)}$

$Ϝ\left({\sigma }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\sigma }_1\mathrm{,}{\varpi }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\sigma }_2\right)+Ϝ\left({\varpi }_1\mathrm{,}{\varpi }_2\right)$

$-\left[\frac{Ϝ\left({\eta }_1\mathrm{,}{\xi }_2\right)+Ϝ\left({\eta }_1\mathrm{,}{\eta }_2\right)+Ϝ\left({\xi }_1\mathrm{,}{\xi }_2\right)+Ϝ\left({\xi }_1\mathrm{,}{\eta }_2\right)}{4}\right]$

$\mathrm{<mo>=</mo>9.9887}\times {10}^{42}\mathrm{.}$ (4.12)

In the third case: $h\left(\tau \right)\mathrm{<mo>=</mo>}\frac{1}{\tau }$

$\frac{1}{16}Ϝ\left({\sigma }_1+{\varpi }_1-\frac{{\xi }_1+{\eta }_1}{2}\mathrm{,}{\sigma }_2+{\varpi }_2-\frac{{\xi }_2+{\eta }_2}{2}\right)\mathrm{<mo>=</mo>7.2025}\times {10}^{19}\mathrm{,}$

$\frac{1}{\left({\eta }_1-{\xi }_1\right)\left({\xi }_2-{\eta }_2\right)}{\displaystyle {\int }_{{\sigma }_1+{\varpi }_1-{\eta }_1}^{{\sigma }_1+{\varpi }_1-{\xi }_1}}{\displaystyle {\int }_{{\sigma }_2+{\varpi }_2-{\xi }_2}^{{\sigma }_2+{\varpi }_2-{\eta }_2}}Ϝ\left(\varkappa \mathrm{,}\gamma \right)d\gamma d\varkappa \mathrm{<mo>=</mo>5.3422}\times {10}^{31}\mathrm{.}$

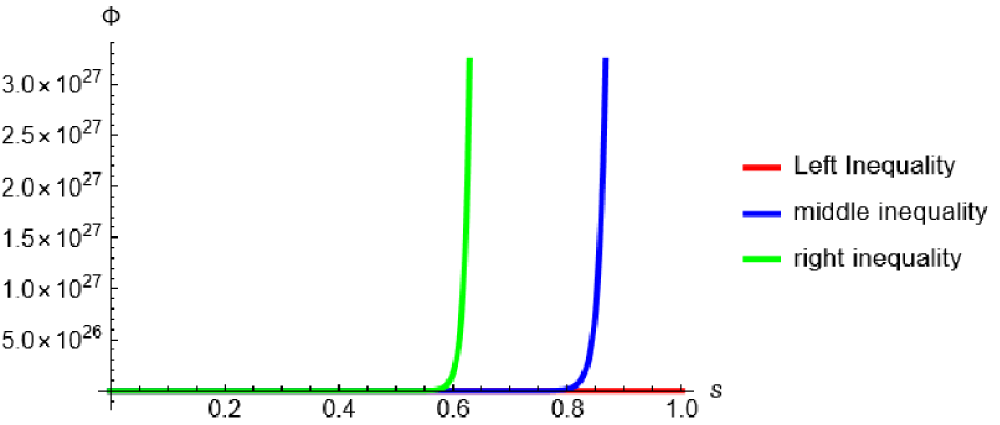
From inequalities (4.17)-(4.12), we can conclude that inequalities of Theorem 3 are better when $s\to 0$ and worse when $s\to 1.$

Remark 5

Clearly, in Example 2, from Table 1 and Figure 1 our newly established inequalities give better results when $s\to 0.$  

Remark 6

Clearly, in Example 3, from Table 2 and Figure 2our newly established inequalities give better results when $s\to 0.$  

5. Applications

Hermite-Hadamard–Mercer inequality has several applications in mathematical analysis and optimization. Here are some potential areas of application:

1. Mathematical analysis

Hermite-Hadamard–Mercer inequality provides tighter bounds and more precise estimates, enhancing theoretical understanding and practical applications. General convex functions offer insights into broader applications where traditional convexity concepts are insufficient.

2. Optimization

Improved inequalities can enhance the performance and accuracy of optimization algorithms, especially those that rely on convexity assumptions. In operations research, refined inequalities can lead to more efficient solutions for resource allocation problems by providing better bounds and estimates.

3. Computational analysis

Computational analysis of these inequalities can help in developing numerical methods that are more efficient and accurate. Refined inequalities can improve the fidelity of simulations and models that involve convex functions or require precise bounds for their operations.

4. Economics and finance

In financial mathematics, tighter inequalities can improve risk assessments and pricing models by providing more accurate estimates. Enhanced convex function analysis can refine economic models, leading to better predictions and insights.

5. Engineering

In control theory, refined inequalities can lead to more precise control algorithms, improving system stability and performance. Better bounds and estimates can improve signal processing techniques, leading to clearer and more accurate results.

6. Conclusion

In this article, we demonstrated the Jensen-Mercer inequality for coordinated h-convex functions and introduced the novel Hermite–Hadamard-Mercer type inequalities tailored for coordinated h-convex functions, leveraging a newly discovered inequality. We provided numerical examples and conducted computational analyses of the derived inequalities, showcasing their superior estimation capabilities compared to previously established results. This work significantly contributes to the evolution of mathematical theory and its real-world applications by effectively connecting theoretical concepts with practical problem-solving methodologies. It represents a fresh trajectory in the realm of inequalities, offering valuable insights for researchers immersed in this domain.

Authors contributions

Conceptualization, Methodology, Validation, Investigation, Writing-original Draft preparation: All these were done by M. Toseef. Writing-review and editing, M. Toseef, A. Mateen, H. Budak, A. Kashuri, Visualization: M. Toseef, A. Mateen, H. Budak, A. Kashuri, Supervision: Z. Zhang, Project administration: Z. Zhang and H. Budak. All authors have read and agreed to the final version of the manuscript.