Annals of Mathematics and Physics
Beam Dynamic Equations for Predictive Modeling of Semicircular Canal Pathologies
Yves Gourinat* and Marie-Stéphane Guillaumont
Cite this as
Gourinat Y, Guillaumont MS. Beam Dynamic Equations for Predictive Modeling of Semicircular Canal Pathologies. Ann Math Phys. 2024;7(2):232-234. Available from: 10.17352/amp.000127Copyright Licence
© 2024 Gourinat Y, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.This short paper presents a general strategy devoted to an original analytical approach of looped 1.5D equations. It considers particular properties of rod/beam equations for wave and structural modal representation. Specific boundary conditions introduce local singularities representing discontinuities and inversions. The process presented in the paper links this kind of original analysis with possible models of the physiological and pathological dynamic behavior of solid-fluid interaction in inner-ear elements such as the anterior and superior semicircular canals. Thus, these models propose a robust representation of these elements, offering observation/control perspectives for diagnostics and cure.
Introduction
This paper presents an original strategy for implementing the dynamic equations of beams in a doubly innovative configuration. Starting with the generic Bresse and Lagrange equations and solutions, the boundary conditions are topologically looped back from bars and beams to rings and closed structures. To this is added the introduction of active or passive singularities, which introduce discontinuities into the modal solutions. This mathematical approach enables the analytical modeling of complex systems derived from biodynamics, such as semicircular canals and otoliths. It offers a predictive model for physiology, dynamic diagnosis of certain pathologies, and robust analysis of active or passive disturbances in complex living systems.
The advantages obtained by this approach are both mathematical and physiological. First, concerning the singularities, Dirichlet’s type (with continuous, broken, or inversed deflections) and Neumann’s type (with continuous, broken, or inversed stresses) give a panel of solutions with a significant number of combinations. This approach benefits from the fact that 1.5D equations raise generic solutions, with Euler and Lagrange parameters, in which the constants can be defined by boundary conditions or singularities. Secondly, the boundary conditions and singularities correspond to physiological and pathological situations. The boundary conditions are generated by the anatomic configurations, and the singularities match window-type pathologies, dehiscent situations, and neuritis pathologies. Last but not least, the local singularities and pathological items induce global consequences that are typically represented by the generic proposed solutions [1].
Wave and structural equations of open and closed beams
In a longitudinally loaded bar, the longitudinal displacement U gives rise to a generic harmonic solution:
In a long beam in flexion, the lateral displacement V implies a circular and hyperbolic spatial function:
All the constitutive equations are classical Euler and Lagrange Rod and Beam models, detailed in ref [2]. It appears clear that, with a second and fourth-order constitutive differential equation, with the Lagrangians separation of time-space functions, we obtain generic shapes with two and four real constants. All the process is founded on this approach, in which the boundary conditions and singularities (and thus physiological and pathological situations) are represented.
These two types of equations correspond respectively to Helmholz modes and thin-structure modes, and are therefore complementary for analytically modeling, as a first approach, any dynamic system in which one dimension is large relative to the others.
Generic solutions can be looped in the sense of Dirichlet (continuity of displacements, Lagrange representation) or Neumann (continuity of force flows, Euler representation). It thus gives ring solutions in wave modes (Schrödinger modes) or bending modes (structural modes), as shown in the mode illustrated in Figure 1 below, where both conditions are met:
These solutions can of course be made more complex by decomposing the ring into elementary segments with different (but constant) characteristics, and by adding viscous damping. These extensions do not alter the essential strategy of the model, which is based on topological looping.
Introduction of singular elements
In this analytical model, we propose to introduce a Dirichlet or Neumann discontinuity singularity (Figure 2), leading to discontinuous modes. In this way, we can represent a mechanical continuity, and if we then introduce a Dirichlet or Neumann multiplicative factor that can take on a negative value.
As a result, we have a model capable of analytically representing a dynamic system that is not only topologically looped, but also endowed with localized passive or active faults, whose effects on the overall dynamics can be freely observed.
Link with possible pathologies and biophysics
The semicircular canals are a typical example of a looped living system, the seat of dynamic phenomena, possibly affected by passive or active disturbances. They are made up of complex materials: solids (bone, cartilage, membranes), fluids (endolymph, perilymph) and intermediates. The advantage of an integrated, looped mathematical model is precisely that it takes into account the overall complexity of this system (represented by an equivalent beam material). What's more, having a generic solution makes the model robust to the influence of disturbances on overall behavior.
The simple singularity can represent a pathological window syndrome, and the negative feedback can simulate infectious neuritis. A first field of application for these mathematical models is therefore an aid to modeling, prediction, diagnosis, and even correction of this type of pathology.
The description of the pathologies is given in ref. [3-5]. The general consequence is discontinuities in pressures, geometry, and control, and the nature of the generic obtained mathematical solutions follows this kind of behavior.
In addition, taking into account the analytical model of acoustic and structural modes places the dynamic system in its global physical environment. This enables us to predict couplings with the local dynamic environment. In this way, the vestibule - of which the semicircular canals are a major component, and which performs a balancing function - can be linked to acoustic measurements and thus coupled to neighboring elements grouped in the cochlea. A matrix of physiological and pathological correspondences between the various elements, measures, and actuators of the inner ear can thus be drawn up.
Conclusion
In the pathological domain, experiments are delicate but, as shown in references, observations have been made in various situations. In the frame of the present models, that have been mathematically developed, it has been shown that, on one hand, this kind of approach represents identified diseases, and on the other hand that it could be proposed for future tests and prediction of curing situations: surgical operation, additional material elements, prosthetic approach. The proposed model has the advantage of providing a dynamic robust representation of singular situations. The interest is, for the mathematician and mechanician, to explore specific combinations of the constants in generic solutions. The interest in life science is to join usual pathological situations with a possible exploration of diagnosis and care.
- Miguel C, Núñez IF, Gourinat Y, Matignon D. Port-Hamiltonian formulations of some elastodynamics theories of isotropic and linearly elastic shells: Naghdi–Reissner’s moderately thick shells. Appl Sci. 2023;13(4):2608 Available from: https://www.mdpi.com/2076-3417/13/4/2608.
- Gourinat Y, Rolland A, Hanchin T. Constitutive equations of structural dynamics. Course M2 level, ISAE; 2024;144.
- Iversen M, Rabbitt R. Wave mechanics of the vestibular semicircular canals. Biophys J. 2017;113(5):1133-1149.Available from: https://doi.org/10.1016/j.bpj.2017.08.001
- Graf W, Klam F. The vestibular system: comparative and functional anatomy, evolution and development. 2006;5(3-4):637-655. Available from: https://www.sciencedirect.com/science/article/pii/S1631068305001867.
- Vidal C. Dizziness and disorders of balance. Accessed July 18, 2024. Available from: https://www.docteurvidal-iec.com/otoneurologie/vertiges.html.
Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
 Help ?
Help ?

PTZ: We're glad you're here. Please click "create a new query" if you are a new visitor to our website and need further information from us.
If you are already a member of our network and need to keep track of any developments regarding a question you have already submitted, click "take me to my Query."

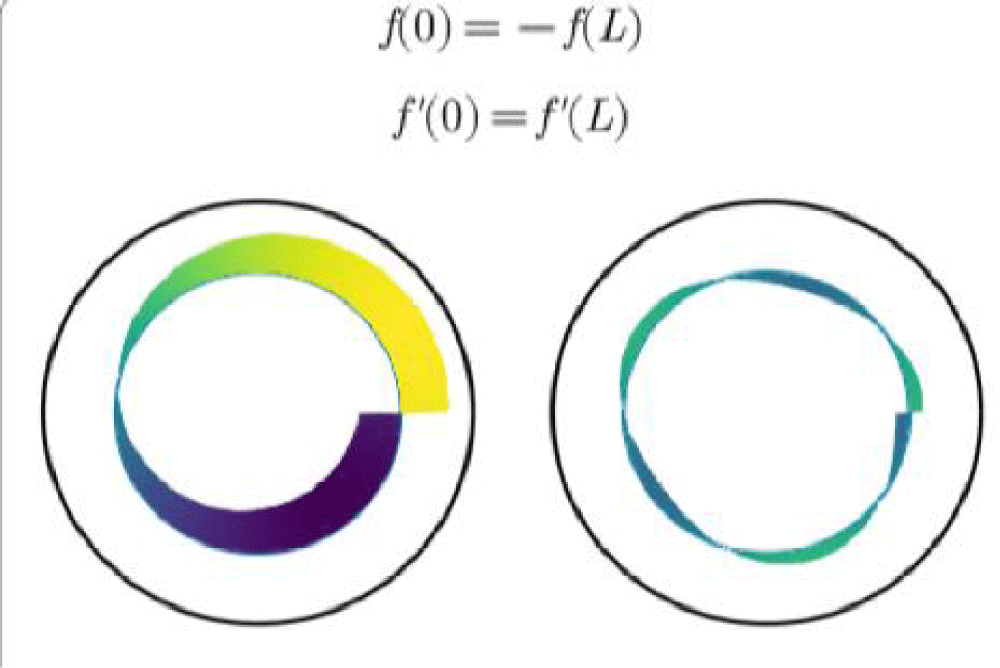


 Save to Mendeley
Save to Mendeley